Inverted Prism

from pathlib import Path
import os
import functools
import itertools
import time

from IPython.display import HTML, Image, Video
import matplotlib.pyplot as plt
import numpy as np
from celluloid import Camera
import matplotlib.patches as patches
from scipy.integrate import odeint, solve_ivp
from simple_pid import PID
from tqdm import tqdm

ROOT = Path("./assets/img/")

if not os.path.exists(ROOT):
    os.makedirs(ROOT)

\[\tau = I \alpha\] \[\tau = rF \sin(\theta)\] \[\frac{d \omega}{dt} = \frac{r F}{I} \sin(\theta)\] \[\frac{d \theta}{dt} = \omega\]

deg = np.rad2deg
rad = np.deg2rad

L = 1.
r = L/(2*np.cos(rad(30)))
m = 1.
I = m*r**2
g = -1.
MAX_THETA = rad(60.)

def plot_prism(theta, ax):

    vertices = np.array([
        [0, 0],
        [-L*np.cos(rad(60)), L*np.sin(rad(60))],
        [L*np.cos(rad(60)), L*np.sin(rad(60))],
        [0, 0],
    ])

    R = np.array([[np.cos(theta), -np.sin(theta)], 
                  [np.sin(theta), np.cos(theta)]])
    vertices = (R@vertices.transpose(1,0)).transpose(1,0)
    
    ax.set_xticks([])
    ax.set_yticks([])
    ax.set_xlim((-L, L))
    ax.set_ylim((-L, L))
    ax.hlines(0, xmin=-L, xmax=L, color="black", linestyles="dotted")
    ax.vlines(0, ymin=-L, ymax=L, color="black", linestyles="dotted")
    
    ax.plot(vertices[:,0], vertices[:, 1], color="royalblue")

def inverted_prism_step(t, s, pid=None):
    theta, omega = s

    dtheta = omega
    F = np.abs(m*g)
    domega = r * F/I * np.sin(theta)

    if pid is not None:
        tau = pid(theta)
        domega += tau/I
    
    return np.array([dtheta, domega])

def sim_inv_prism():

    T = 5.
    t = np.linspace(0, T, 200)

    # theta, omega
    s0 = np.array([0., 0.1])
    
    def stop_event(t, y):
        return np.abs(y[0]) - MAX_THETA
    
    stop_event.terminal = True
    
    sol = solve_ivp(inverted_prism_step, (0, T), s0, t_eval=t, 
                    events=stop_event)
    sol = sol.y.transpose(1,0)
    
    fig, ax = plt.subplots(1,1)

    camera = Camera(fig)
    
    for theta, _ in sol:
        plot_prism(theta, ax=ax)
        
        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "inv_prism.gif"  
    anim.save(gif_path, writer="pillow", fps=10)
    return Image(url=gif_path)
    
sim_inv_prism()

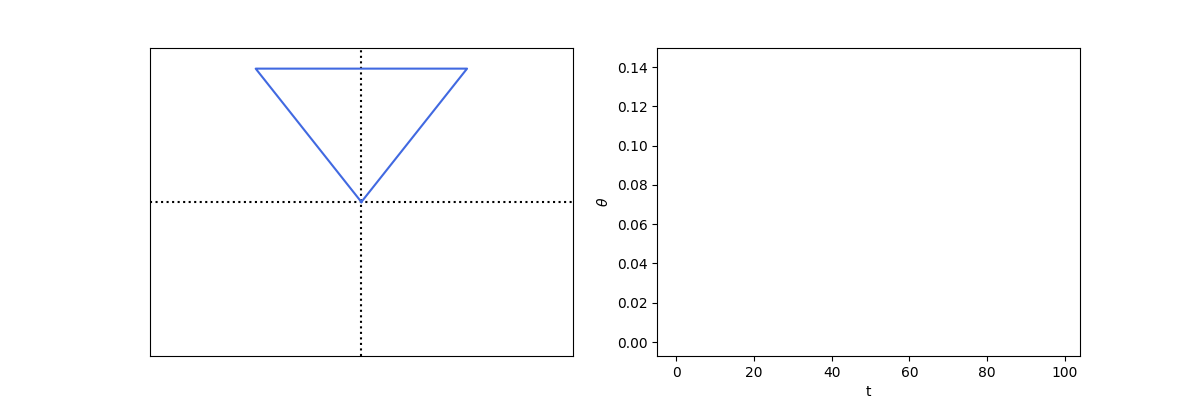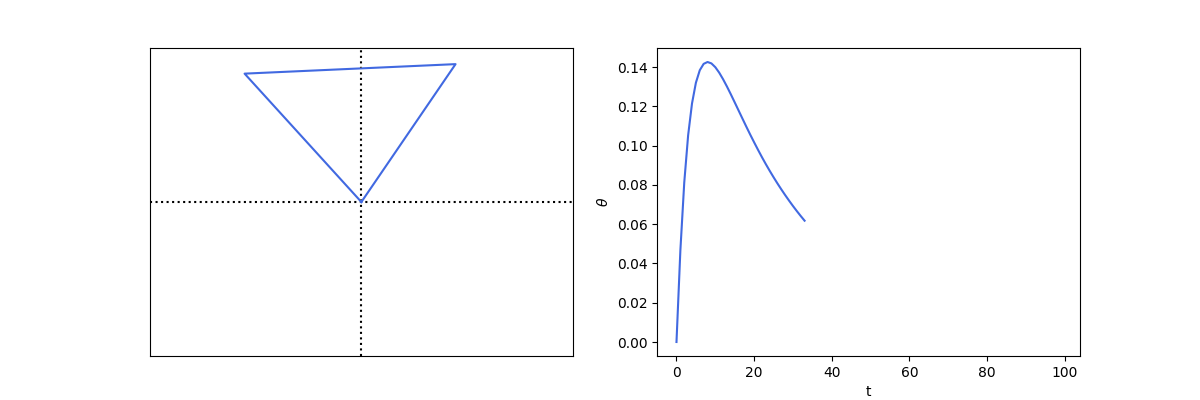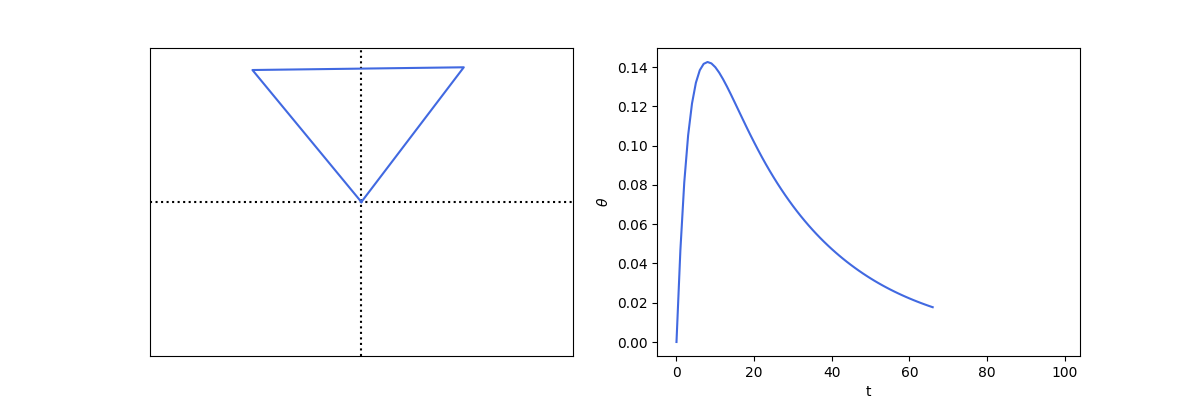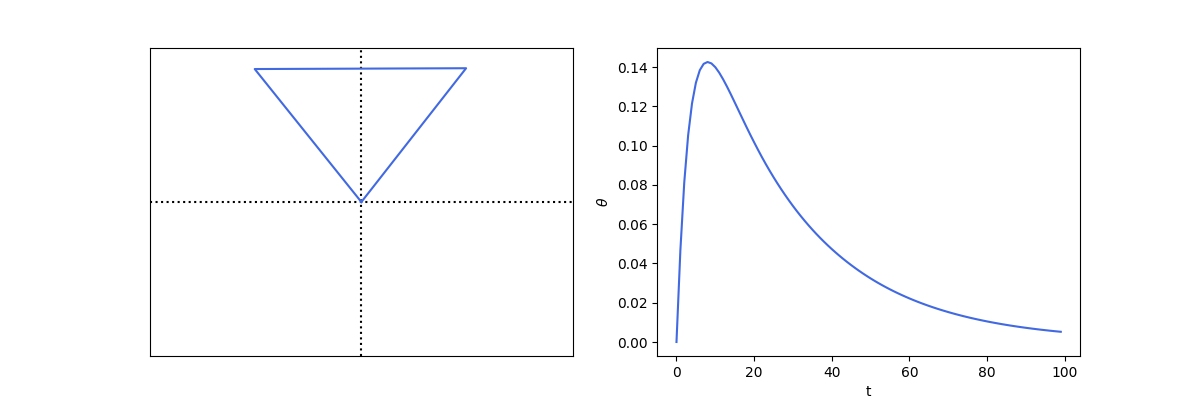
Stabilising using PID

def control_inv_prism():

    T = 2.
    t = np.linspace(0, T, 100)

    # theta, omega
    s0 = np.array([0., 2.5])

    pid = PID(10., .1, .05, setpoint=0.)
    pid.sample_time = 0.
    
    def stop_event(t, y):
        return np.abs(y[0]) - MAX_THETA
    
    stop_event.terminal = True
    
    sol = solve_ivp(functools.partial(inverted_prism_step, pid=pid), 
                                      (0, T), s0, t_eval=t, events=stop_event)
    sol = sol.y.transpose(1,0)
    
    fig, axes = plt.subplots(1, 2, figsize=(12,4))
    axes[1].set_xlabel("t")
    axes[1].set_ylabel(r"$\theta$")

    camera = Camera(fig)
    
    for t_idx, (theta, _) in enumerate(sol):
        plot_prism(theta, ax=axes[0])
        axes[1].plot(range(t_idx+1), sol[:t_idx+1, 0], color="royalblue")
        
        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "control_inv_prism.gif"  
    anim.save(gif_path, writer="pillow", fps=10)
    return Image(url=gif_path)
    
control_inv_prism()