from pathlib import Path
import os
import functools
import itertools
import time

from IPython.display import HTML, Image, Video, Audio
import matplotlib.pyplot as plt
import numpy as np
from celluloid import Camera
import matplotlib.patches as patches
from scipy.integrate import odeint, solve_ivp
from simple_pid import PID
from tqdm import tqdm
from scipy.io import wavfile
from scipy.signal import resample

ROOT = Path("./assets/img/")

if not os.path.exists(ROOT):
    os.makedirs(ROOT)

def show_img(fig, path):
    fig.savefig(path)
    return Image(url=path)

R = 1.
A = 1.
c = 1.
center = np.array([0., 0.])
sigma = 0.2
h = 0.01

def plot_surface(X, Y, u, ax):
    ax.plot_surface(X, Y, u, color="olivedrab")

def pad(a):
    return np.pad(a, ((1, 1), (1, 1)), 'constant', constant_values=0)

def sim_2d_wave():

    X = np.arange(-R, R, h)
    Y = np.arange(-R, R, h)
    X, Y = np.meshgrid(X, Y)

    u0 = A*np.exp(-((X - center[0])**2 + (Y - center[1])**2)/sigma**2)
    inside = (X**2 + Y**2 < R**2)
    u0[~inside] = 0.

    dt = 0.7*h/(c*np.sqrt(2))

    Lambda = c*dt/h

    T = 5.

    u0 = pad(u0)
    rows, cols = u0.shape
    sol = [u0, u0]
    for _ in tqdm(enumerate(np.arange(0, T+dt, dt))):

        u_prev = sol[-1]
        u_prev_2 = sol[-2]

        u_new = 2*u_prev[1:-1,1:-1] - u_prev_2[1:-1,1:-1] + \
            Lambda**2*(u_prev[2:,1:-1] + u_prev[:-2,1:-1] + u_prev[1:-1,2:] + u_prev[1:-1,:-2] - 4*u_prev[1:-1,1:-1])
        
        u_new = pad(u_new)

        u_new[1:-1,1:-1][~inside] = 0.
        sol.append(u_new)
    
    fig = plt.figure(figsize=(8,8))
    ax = fig.add_subplot(projection='3d')

    ax.set_xlim(-R, R)
    ax.set_ylim(-R, R)
    ax.set_zlim(-A, A)  # or auto, but fixed looks more stable in animation
    ax.set_box_aspect((1, 1, 0.3))
    ax.set_xticklabels([])
    ax.set_yticklabels([])
    ax.set_zticklabels([])
    
    camera = Camera(fig)

    step = max(len(sol) // 150, 1)
    
    for u in tqdm(sol[::step]):

        u = u[1:-1, 1:-1]
        u = np.ma.array(u, mask=~inside)
        
        plot_surface(X, Y, u, ax=ax)
        
        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "2d_wave.gif"  
    anim.save(gif_path, writer="pillow", fps=10)
    return Image(url=gif_path), sol

img, sol = sim_2d_wave()

img

def sample_displacement(sol):

    cx = sol[0].shape[0] // 2
    cy = sol[0].shape[1] // 2

    sample = []
    for u in sol:
        sample.append(u[cx, cy])
    return np.array(sample)

sample = sample_displacement(sol)

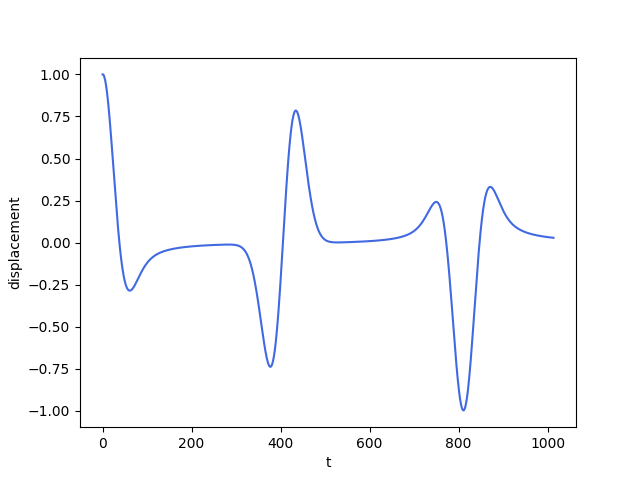
def plot_sample(sample):

    t = np.arange(len(sample))

    fig = plt.figure()
    ax = plt.subplot()

    ax.set_xlabel("t")
    ax.set_ylabel("displacement")

    ax.plot(t, sample, color="royalblue")
    plt.close()

    return show_img(fig, path=ROOT/"sample.png")

plot_sample(sample)

def to_wave(sample, path, seconds=2.):

    sr = 44100  # samples/second

    x = sample.astype(np.float32)
    
    # normalize to [-1, 1] (avoid clipping)
    x = x - x.mean()
    mx = np.max(np.abs(x))
    if mx > 0:
        x = x / mx

    N = int(seconds * sr)

    x = resample(x, N).astype(np.float32)
    
    fade = 10
    x[:fade] = np.linspace(0, 1, fade)
    x[-fade:] = np.linspace(1, 0, fade)
    
    # convert to int16 for WAV
    x_int16 = (x * 32767).astype(np.int16)
    
    wavfile.write(path, sr, x_int16)
    return Audio(x, rate=sr)

to_wave(sample, path=ROOT/"sample.wav")