Double Pendulum

from pathlib import Path
import os
import functools

from IPython.display import HTML, Image
import matplotlib.pyplot as plt
from numpy import *
from celluloid import Camera
import matplotlib.patches as patches
from scipy.integrate import odeint, solve_ivp
from simple_pid import PID

ROOT = Path("./assets/img/")

if not os.path.exists(ROOT):
    os.makedirs(ROOT)

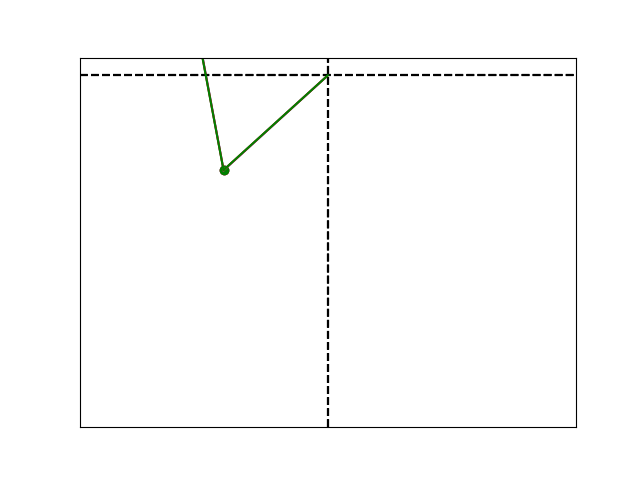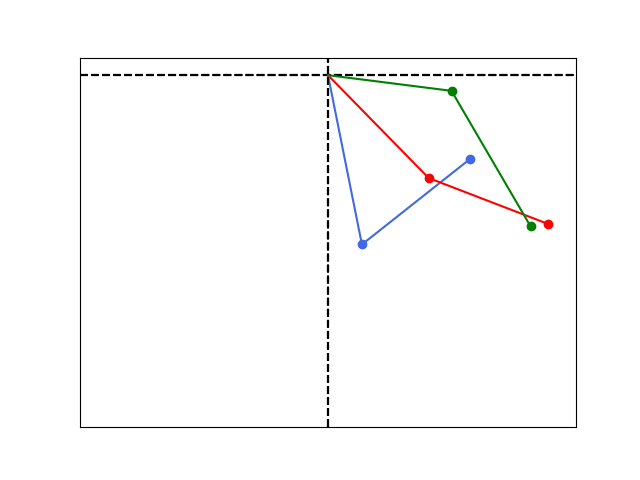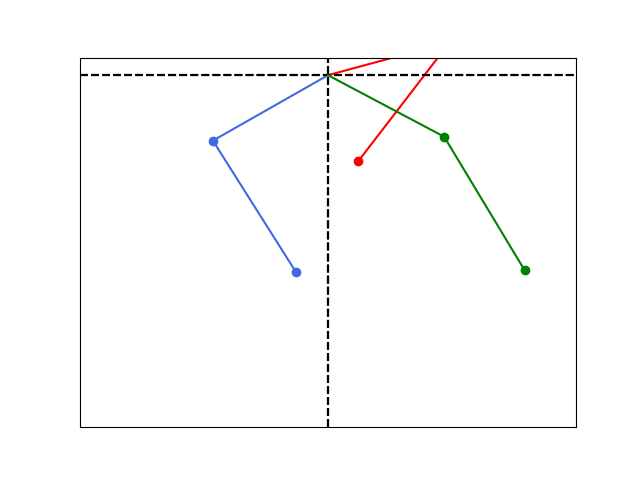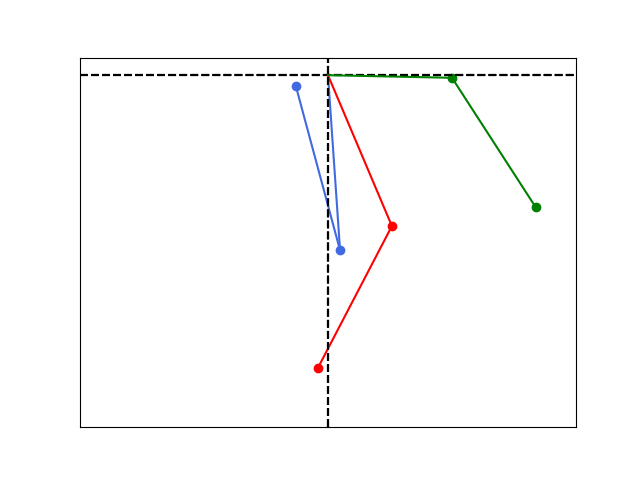
A double pendulum.

L1 = 1.
L2 = 1.
m1 = 1.
m2 = 1.
g = -9.81

XMIN = -L1-L2
XMAX = L1+L2
YMIN = -L1-L2
YMAX = 0.1

def show_fig(fig, tag):
    png_path = ROOT / f"{tag}.png"  
    fig.savefig(png_path)
    return Image(url=png_path)

def plot_pend(theta1, theta2, ax=None, color="black"):

    if ax is None:
        ax = plt.subplot()

    x_m1 = L1*sin(theta1)
    y_m1 = -L1*cos(theta1)

    x_m2 = x_m1 + L2*sin(theta2)
    y_m2 = y_m1 - L2*cos(theta2)

    ax.set_xticks([])
    ax.set_yticks([])

    ax.set_xlim((XMIN, XMAX))
    ax.set_ylim((YMIN, YMAX))

    ax.hlines(0., xmin=XMIN, xmax=XMAX, color="black", linestyles="dashed")
    ax.vlines(0., ymin=YMIN, ymax=YMAX, color="black", linestyles="dashed")

    ax.plot([0, x_m1], [0, y_m1], color=color)
    ax.plot([x_m1, x_m2], [y_m1, y_m2], color=color)
    ax.scatter([x_m1, x_m2], [y_m1, y_m2], color=color)

    fig = ax.get_figure()
    plt.close()

    return fig

show_fig(plot_pend(theta1=1., theta2=2.), tag="double_pend",)

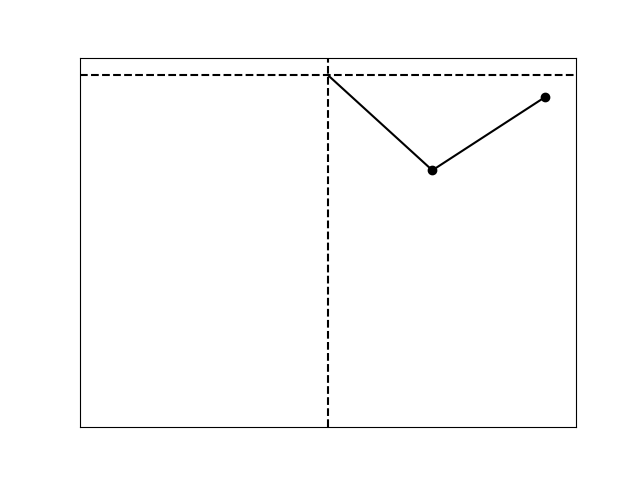
Let $L_1$ and $L_2$ be the lengths of the upper and lower arms, respectively, $m_1$ and $m_2$ the upper and lower masses, $\theta_1$ and $\theta_2$ the angles between the upper and lower arms and the vertical, $g = -9.81$ the gravity acceleration, $x_1$, $y_1$, $x_2$, $y_2$ the $x,y$ coordinates of the upper and lower masses.

\[\begin{align*} g m_1+T_1 \cos \left(\theta _1\right)-T_2 \cos \left(\theta _2\right)&=-L_1 m_1 \left(\dot{\theta }_1^2 \left(-\cos \left(\theta _1\right)\right)-\ddot{\theta }_1 \sin \left(\theta _1\right)\right)\\\\ T_2 \sin \left(\theta _2\right)-T_1 \sin \left(\theta _1\right)&=L_1 m_1 \left(\ddot{\theta }_1 \cos \left(\theta _1\right)-\dot{\theta }_1^2 \sin \left(\theta _1\right)\right)\\\\ g m_2+T_2 \cos \left(\theta _2\right)&=m_2 \left(-L_1 \left(\dot{\theta }_1^2 \left(-\cos \left(\theta _1\right)\right)-\ddot{\theta }_1 \sin \left(\theta _1\right)\right)-L_2 \left(\dot{\theta }_2^2 \left(-\cos \left(\theta _2\right)\right)-\ddot{\theta }_2 \sin \left(\theta _2\right)\right)\right)\\\\ T_2 \left(-\sin \left(\theta _2\right)\right)&=m_2 \left(L_1 \left(\ddot{\theta }_1 \cos \left(\theta _1\right)-\dot{\theta }_1^2 \sin \left(\theta _1\right)\right)+L_2 \left(\ddot{\theta }_2 \cos \left(\theta _2\right)-\dot{\theta }_2^2 \sin \left(\theta _2\right)\right)\right) \end{align*}\]

Eliminating $T_1$ and $T_2$ and using:

\[\begin{align*} x_1 &= L_1 \sin \left(\theta _1\right)\\\\ y_1 &= L_1 \left(-\cos \left(\theta _1\right)\right)\\\\ x_2 &= L_1 \sin \left(\theta _1\right)+L_2 \sin \left(\theta _2\right)\\\\ y_2 &= L_1 \left(-\cos \left(\theta _1\right)\right)-L_2 \cos \left(\theta _2\right) \end{align*}\]

We get:

\[\begin{align*} \ddot{\theta }_1 &= \frac{g \left(2 m_1 \sin \left(\theta _1\right)+m_2 \sin \left(\theta _1\right)+m_2 \sin \left(\theta _1-2 \theta _2\right)\right)+\dot{\theta }_1^2 L_1 m_2 \left(-\sin \left(2 \left(\theta _1-\theta _2\right)\right)\right)-2 \dot{\theta }_2^2 L_2 m_2 \sin \left(\theta _1-\theta _2\right)}{L_1 \left(-m_2 \cos \left(2 \left(\theta _1-\theta _2\right)\right)+2 m_1+m_2\right)}\\\\ \ddot{\theta }_2 &= \frac{2 \sin \left(\theta _1-\theta _2\right) \left(-g \left(m_1+m_2\right) \cos \left(\theta _1\right)+\dot{\theta }_1^2 L_1 \left(m_1+m_2\right)+\dot{\theta }_2^2 L_2 m_2 \cos \left(\theta _1-\theta _2\right)\right)}{L_2 \left(-m_2 \cos \left(2 \left(\theta _1-\theta _2\right)\right)+2 m_1+m_2\right)} \end{align*}\]

Rewriting for simulation:

\[\begin{align*} \dot{\omega }_1 &= \frac{g \left(2 m_1 \sin \left(\theta _1\right)+m_2 \sin \left(\theta _1\right)+m_2 \sin \left(\theta _1-2 \theta _2\right)\right)+L_1 m_2 \omega _1^2 \left(-\sin \left(2 \left(\theta _1-\theta _2\right)\right)\right)-2 L_2 m_2 \omega _2^2 \sin \left(\theta _1-\theta _2\right)}{L_1 \left(-m_2 \cos \left(2 \left(\theta _1-\theta _2\right)\right)+2 m_1+m_2\right)}\\\\ \dot{\omega }_2 &= \frac{2 \sin \left(\theta _1-\theta _2\right) \left(-g \left(m_1+m_2\right) \cos \left(\theta _1\right)+L_2 m_2 \omega _2^2 \cos \left(\theta _1-\theta _2\right)+L_1 \left(m_1+m_2\right) \omega _1^2\right)}{L_2 \left(-m_2 \cos \left(2 \left(\theta _1-\theta _2\right)\right)+2 m_1+m_2\right)}\\\\ \omega_1 &= \dot{\theta}_1\\\\ \omega_2 &= \dot{\theta}_2 \end{align*}\]

def double_pend_step(s, t):

    def sec(angle):
        return 1/cos(angle)

    def cot(angle):
        return 1/tan(angle)

    def csc(angle):
        return 1/sin(angle)
    
    theta1, theta2, omega1, omega2 = s


    dtheta1 = omega1
    dtheta2 = omega2

    domega1 = (g*(2*m1*sin(theta1) + m2*sin(theta1) +m2*sin(theta1 - 2*theta2)) 
               +L1*m2*omega1**2*(-sin(2*(theta1-theta2))) -2*L2*m2*omega2**2*sin(theta1-theta2))/(
               L1*(-m2*cos(2*(theta1-theta2)) + 2*m1 + m2))
    domega2 = (2*sin(theta1-theta2)*(-g*(m1+m2)*cos(theta1) +L2*m2*omega2**2*cos(theta1-theta2)+L1*(m1+m2)*omega1**2))/(
        L2*(-m2*cos(2*(theta1-theta2)) +2*m1+m2))

    return array([dtheta1, dtheta2, domega1, domega2])

def sim_double_pend():

    T = 20
    t = linspace(0, T, 200)

    # theta1, theta2, omega1, omega2
    s0 = array([-1., 3.4, 0., 0.])
    
    sol = odeint(double_pend_step, s0, t)
    
    fig, ax = plt.subplots(1,1)

    camera = Camera(fig)
    
    for theta1, theta2, _, _ in sol:
        plot_pend(theta1=theta1, theta2=theta2, ax=ax)
        
        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "double_pend.gif"  
    anim.save(gif_path, writer="pillow", fps=10)
    return Image(url=gif_path)

sim_double_pend()

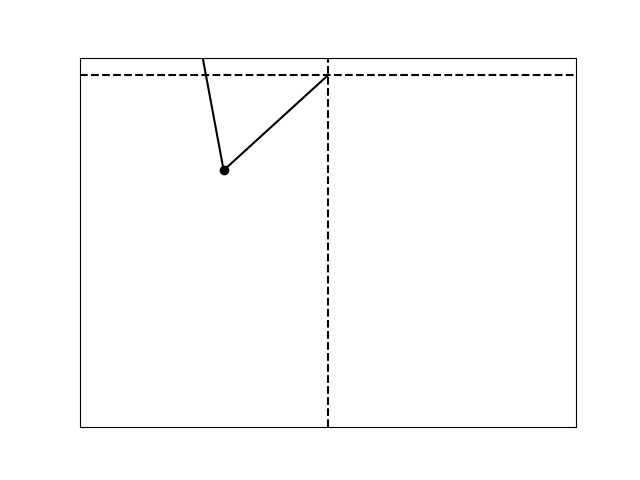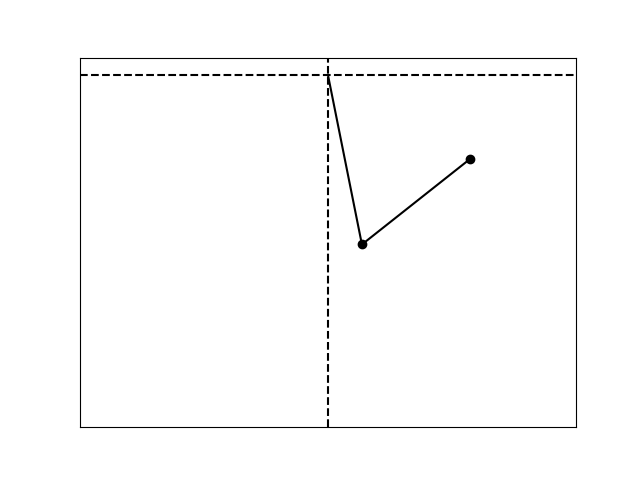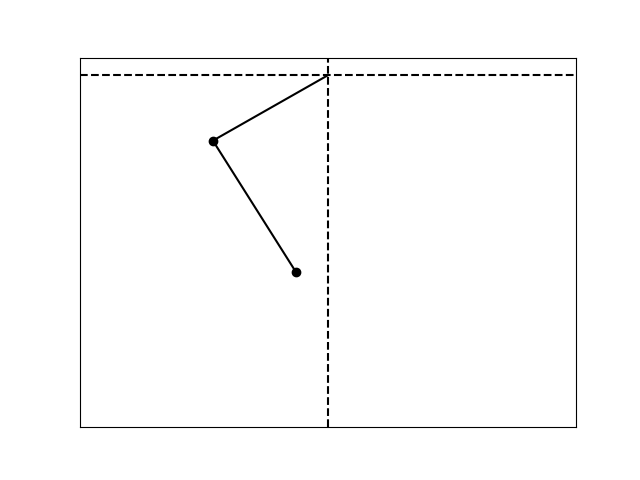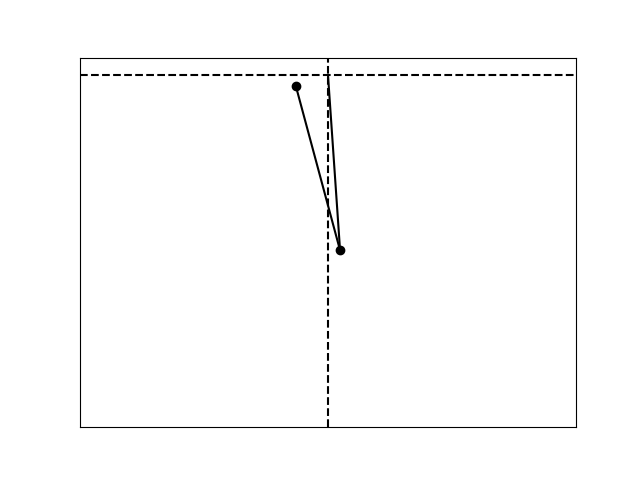
Sensitive dependence on initial conditions.

def sim_double_pend_initial():

    T = 20
    t = linspace(0, T, 200)

    # theta1, theta2, omega1, omega2
    s0 = array([[-1., 3.4, 0., 0.],
                [-1.001, 3.401, 0., 0.],
                [-1.002, 3.402, 0., 0.]])

    solutions = []

    for inital_condition in s0:
        solutions.append(odeint(double_pend_step, inital_condition, t))

    colors = ["royalblue", "red", "green"]

    fig, ax = plt.subplots(1, 1)

    camera = Camera(fig)

    for time_idx in range(len(t)):
        for condition_idx in range(3):
            theta1, theta2, _, _ = solutions[condition_idx][time_idx]
            plot_pend(theta1=theta1, theta2=theta2,
                      ax=ax, color=colors[condition_idx])

        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "double_pend_initial.gif"
    anim.save(gif_path, writer="pillow", fps=10)
    return Image(url=gif_path)


sim_double_pend_initial()