from pathlib import Path
import os

from IPython.display import HTML, Image
import matplotlib.pyplot as plt
import numpy as np
from celluloid import Camera

ROOT = Path("./assets/img/")

if not os.path.exists(ROOT):
    os.makedirs(ROOT)

The differential equation for the damped oscillator:

\[\frac{d^2x}{dt^2} + \frac{b}{m} \frac{dx}{dt} + \frac{k}{m}x = 0\]

Let’s take Laplace transform:

\[(s^2 + \frac{b}{m} s + \frac{k}{m}) X(s) - (s+\frac{b}{m}) x(0) - x'(0) = 0\] \[X(s) = \frac{(s+\frac{b}{m}) x(0) + x'(0)}{s^2 + \frac{b}{m} s + \frac{k}{m}}\]

This resolves our solution in the complex domain. We need to take the inverse transform to get the solution in the time domain. This will depend on the zeros of the denumerator. The discriminant of the polynomial in the denumerator is:

\[\frac{b^2}{m^2} - 4 \frac{k}{m}\]

Case 1: Underdamped

\[\begin{align*} & \frac{b^2}{m^2} -4 \frac{k}{m} < 0\\\\ & b^2 < 4 m k \end{align*}\]

Let’s define:

\[\begin{align*} \omega_n = \sqrt{\frac{k}{m}}\\\\ \zeta = \frac{b}{2 \sqrt{m k}} \end{align*}\]

Complete the square:

\[s^2+\frac{b}{m} s + \frac{k}{m} = (s+\frac{b}{2m})^2 + \frac{k}{m} - \frac{b^2}{4 m^2}\] \[\begin{align*} (s+\frac{b}{2m})^2 + \frac{k}{m} - \frac{b^2}{4 m^2} \\ = (s+\zeta \omega_n)^2 + \omega_n^2 (1 - \zeta^2) \\ = (s+\zeta \omega_n)^2 + \omega_d^2 \end{align*}\]

where $\omega_d = \omega_n \sqrt{1-\zeta^2}$

Write the numerator in terms of $\omega_n$ and $\zeta$:

\[x(0) (s + \frac{b}{m}) + x'(0) = x(0) (s + 2 \zeta \omega_n) + x'(0)\]

Hence,

\[X(s) = \frac{x(0) (s + 2 \zeta \omega_n) + x'(0)}{(s+\zeta \omega_n)^2 + \omega_d^2}\] \[X(s) = \frac{x(0) (s + \zeta \omega_n)}{(s + \zeta \omega_n)^2 + \omega_d^2} + \frac{x(0) \zeta \omega_n + x'(0)}{\omega_d} \frac{\omega_d}{(s + \zeta \omega_n)^2 + \omega_d^2}\]

Take the inverse Laplace:

\[x(t) = e^{-\zeta \omega_n t} [ x(0) \cos(\omega_d t) + \frac{x(0) \zeta \omega_n + x'(0)}{\omega_d} \sin(\omega_d t) ]\]

Using:

\[\alpha \cos(\theta) + \beta \sin(\theta) = \gamma \cos(\theta - \phi)\]

where $\gamma = \sqrt{\alpha^2 + \beta^2}$ and $\phi = atan2(\beta, \alpha)$.

Hence we can simplify to:

\[x(t) = A e^{-\frac{b}{2m} t} \cos(\omega_d t - \phi)\]

where $A = \sqrt{x(0)^2 + (\frac{x(0) \zeta \omega_n + x’(0)}{\omega_d})^2}$ and $\phi = atan2(\frac{x(0) \zeta \omega_n + x’(0)}{\omega_d}, x(0))$.

def underdamped_fn(t):
    omega = 1 # rad/sec
    A = 0.2 # m
    b = 0.3
    m = 1.

    T = 3*1/omega*2*np.pi

    t = np.linspace(0, T, 100)
    return A*np.exp(-b/(2*m)*t)*np.cos(omega*t)

def underdamped():

    T = 20.

    t = np.linspace(0, T, 100)
    x = underdamped_fn(t)

    fig, ax = plt.subplots(1, 1, figsize=(6,5))

    ax.set_title("Underdamped")
    
    ax.set_xlabel("t")
    ax.set_ylabel("x")

    ax.set_xlim((0, T))
    ax.set_ylim((-0.2,0.2))

    camera = Camera(fig)

    for idx, ti in enumerate(t):

        ax.plot(t[:idx+1], x[:idx+1], color="royalblue", label="x")
        ax.scatter(ti, x[idx], color="royalblue")
        ax.hlines(0, 0, T, color="black", linestyle="dashed")

        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "underdamped.gif"  
    anim.save(gif_path, writer="pillow", fps=30)
    return Image(url=gif_path)

underdamped()

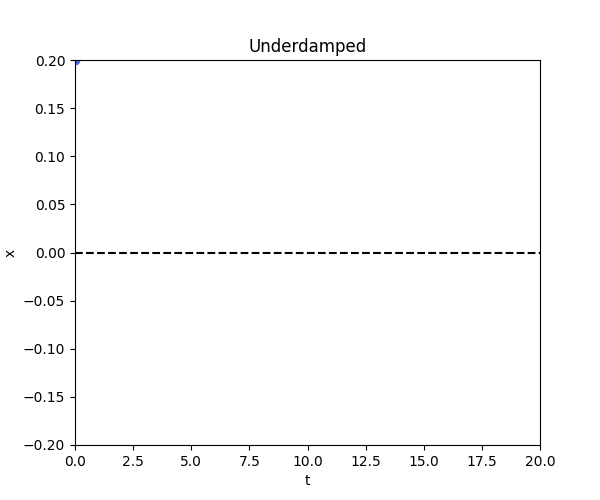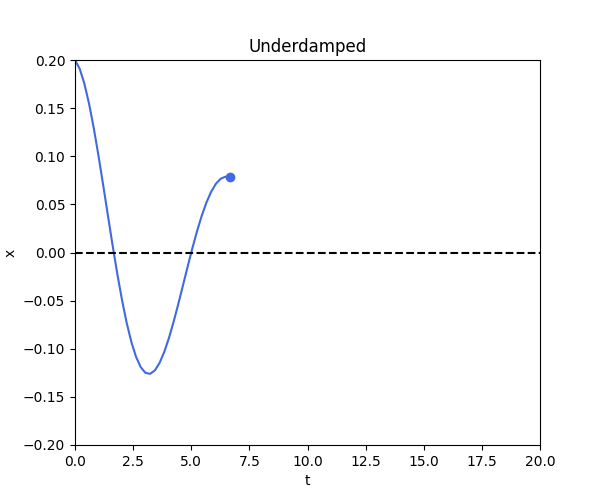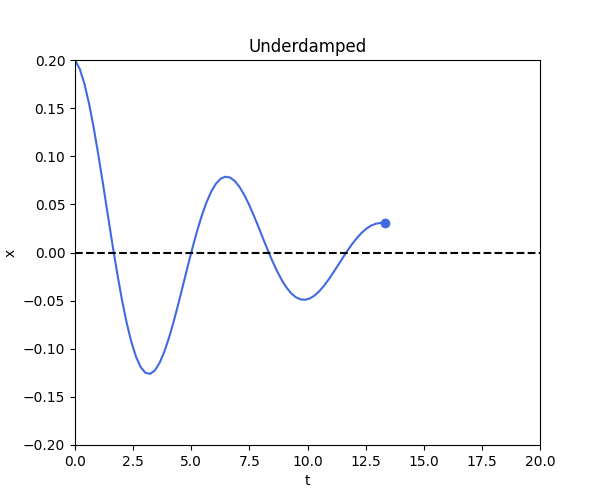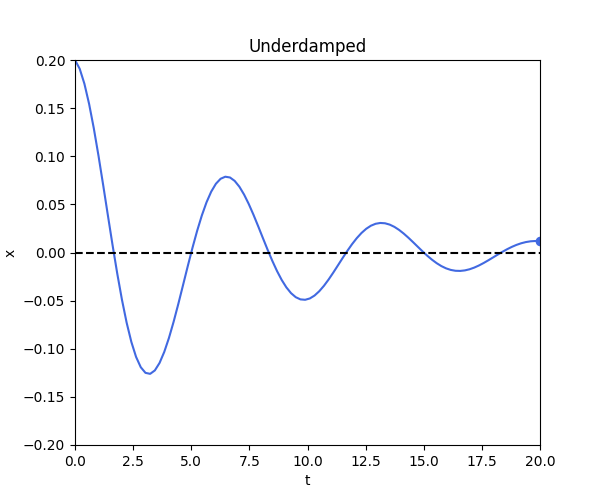
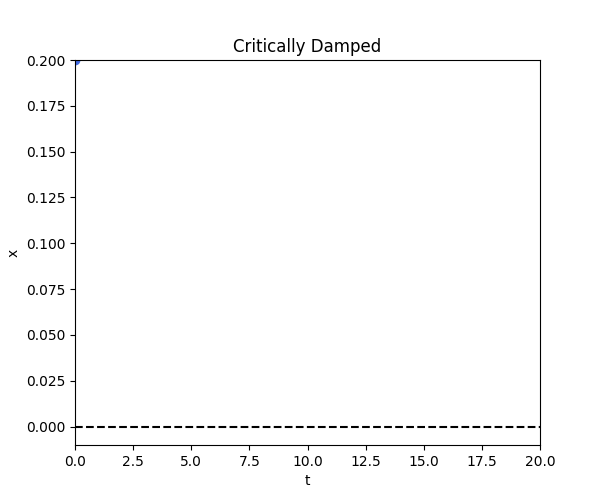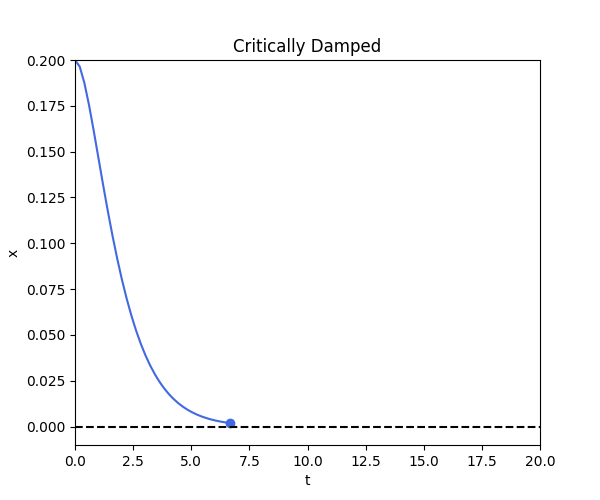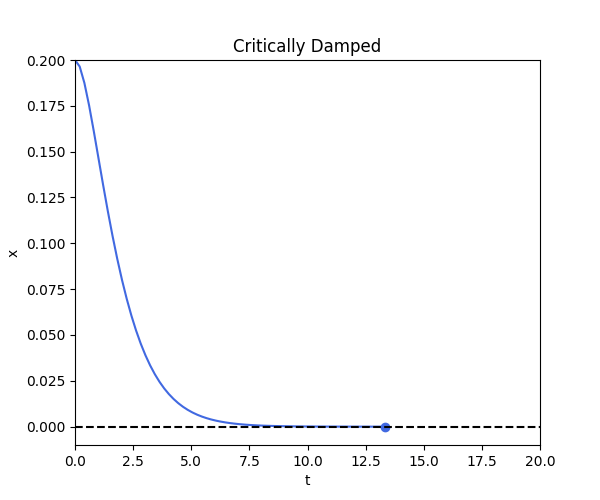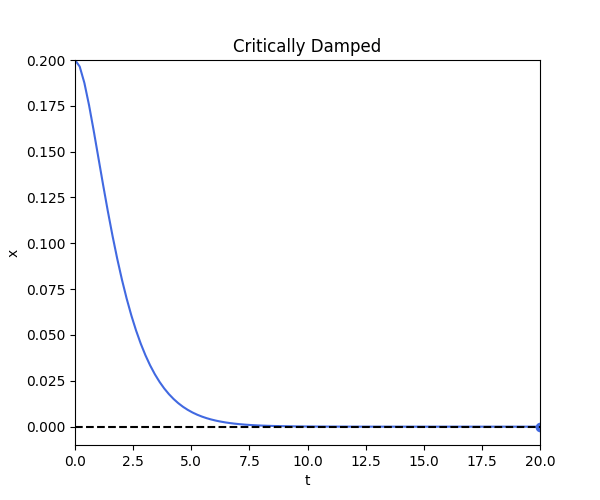
Case 2: Critically Damped

\[\begin{align*} & \frac{b^2}{m^2} -4 \frac{k}{m} = 0\\\\ & b^2 = 4 m k \end{align*}\]

Hence,

\[\begin{align*} s^2+\frac{b}{m} s + \frac{k}{m} = (s + \omega_n)^2 \end{align*}\] \[\begin{align*} X(s) = \frac{(s+ 2\omega_n) x(0) + x'(0)}{(s+\omega_n)^2}\\ X(s) = \frac{x(0)}{s+\omega_n} + \frac{x(0) \omega_n + x'(0)}{(s+\omega_n)^2} \end{align*}\]

Applying the inverse transform:

\[x(t) = [x(0) +( x(0) \omega_n + x'(0))t] e^{-\omega_n t}\]

def critical_damped_fn(t):
    omega = 1 # rad/sec
    A = 0.2

    return A*(1+omega*t)*np.exp(-omega*t)

def critical_damped():

    T = 20
    t = np.linspace(0, T, 100)
    x = critical_damped_fn(t)

    fig, ax = plt.subplots(1, 1, figsize=(6,5))

    ax.set_title("Critically Damped")
    
    ax.set_xlabel("t")
    ax.set_ylabel("x")

    ax.set_xlim((0, T))
    ax.set_ylim((-0.01,0.2))

    camera = Camera(fig)

    for idx, ti in enumerate(t):

        ax.plot(t[:idx+1], x[:idx+1], color="royalblue", label="x")
        ax.scatter(ti, x[idx], color="royalblue")
        ax.hlines(0, 0, T, color="black", linestyle="dashed")

        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "critical_damped.gif"  
    anim.save(gif_path, writer="pillow", fps=30)
    return Image(url=gif_path)

critical_damped()

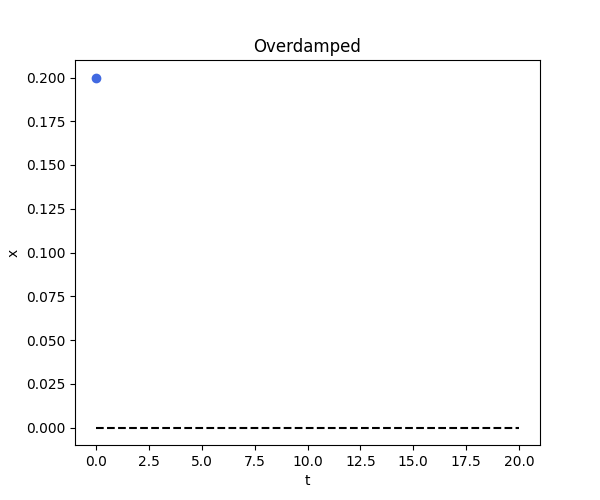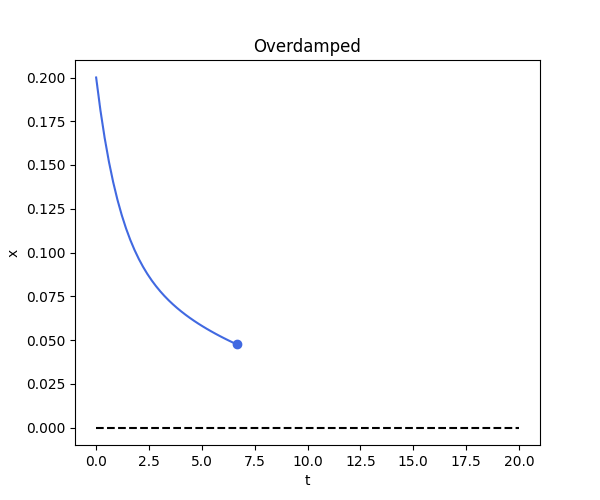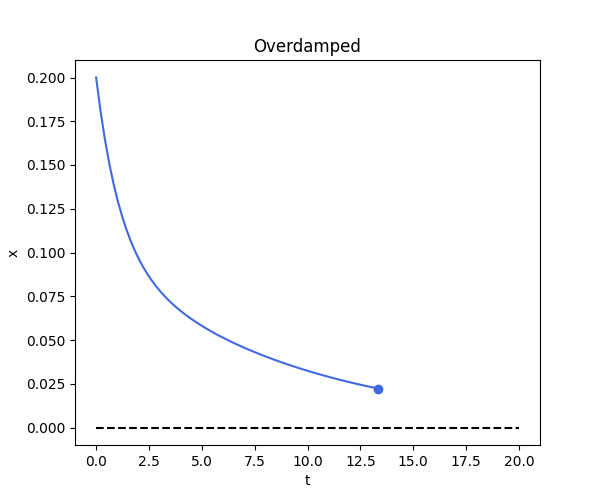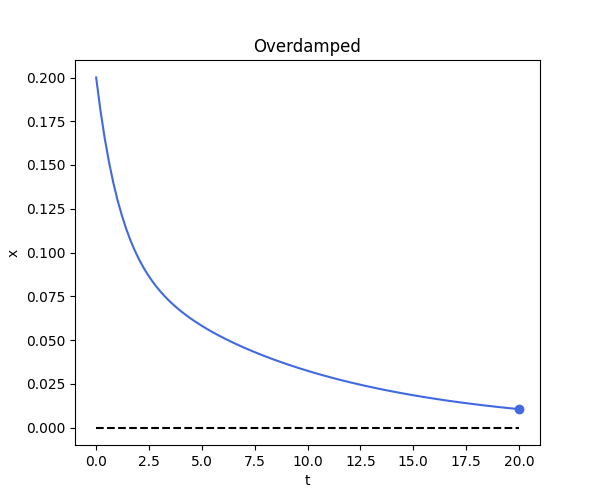
Case 3: Overdamped

\[\begin{align*} & \frac{b^2}{m^2} -4 \frac{k}{m} > 0 \end{align*}\]

The roots of the polynomial in the denumerator is:

\[r_{1,2} = \frac{-\frac{b}{m} \pm \sqrt{\frac{b^2}{m^2} - 4\frac{k}{m}}}{2}\]

Hence,

\[X(s) = \frac{(s+\frac{b}{m}) x(0) + x'(0)}{(s - r_1) (s - r_2)}\]

Using partial fractions,

\[X(s) = \frac{A}{s-r_1} + \frac{B}{s-r_2}\]

Taking inverse transform,

\[x(t) = A e^{r_1 t} + B e^{r_2 t}\]

def overdamped_fn(t):
    b = 1
    m = 1
    k = 0.1

    A = 0.1
    B = 0.1
    
    r1 = (-b/m + np.sqrt(b**2/m**2 - 4*k/m))/2
    r2 = (-b/m - np.sqrt(b**2/m**2 - 4*k/m))/2
    
    return A*np.exp(r1*t) + B*np.exp(r2*t)

def overdamped():
    T = 20
    
    t = np.linspace(0, T, 100)
    x = overdamped_fn(t)

    fig, ax = plt.subplots(1, 1, figsize=(6,5))

    ax.set_title("Overdamped")
    
    ax.set_xlabel("t")
    ax.set_ylabel("x")

    camera = Camera(fig)

    for idx, ti in enumerate(t):

        ax.plot(t[:idx+1], x[:idx+1], color="royalblue", label="x")
        ax.scatter(ti, x[idx], color="royalblue")
        ax.hlines(0, 0, T, color="black", linestyle="dashed")

        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "overdamped.gif"  
    anim.save(gif_path, writer="pillow", fps=30)
    return Image(url=gif_path)

overdamped()

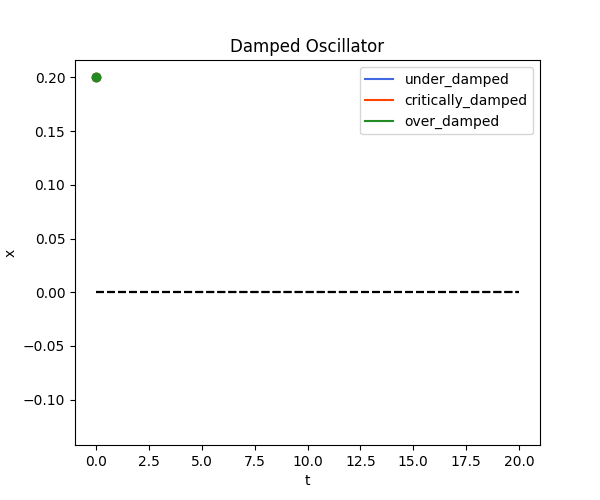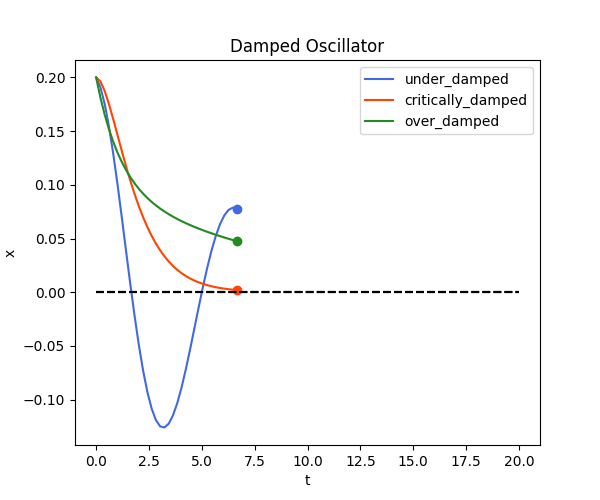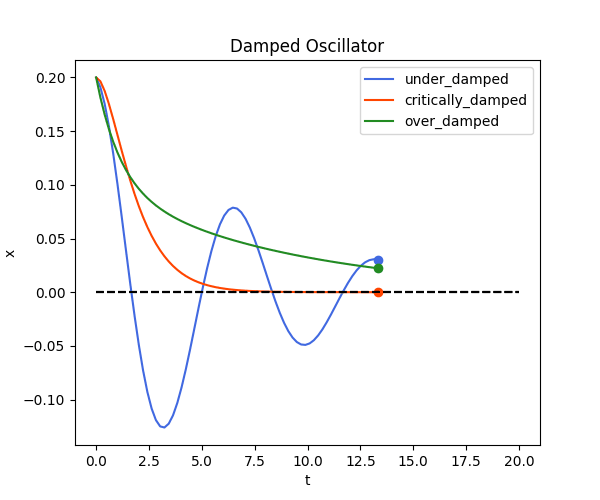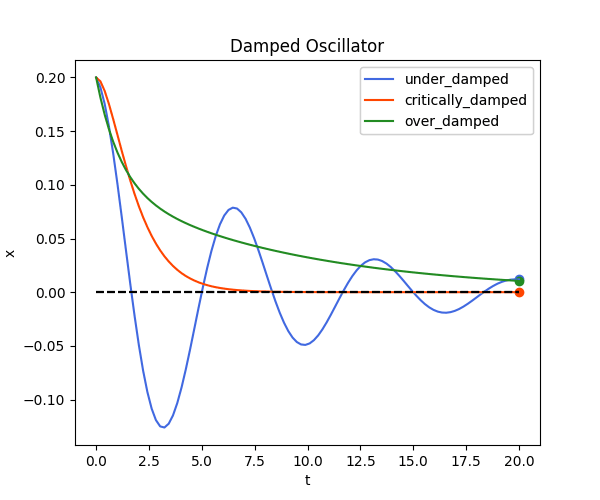
def damped_osc():

    T = 20
    
    t = np.linspace(0, T, 100)

    u_damped = underdamped_fn(t)
    c_damped = critical_damped_fn(t)
    o_damped = overdamped_fn(t)

    fig, ax = plt.subplots(1, 1, figsize=(6,5))

    ax.set_title("Damped Oscillator")
    
    ax.set_xlabel("t")
    ax.set_ylabel("x")

    camera = Camera(fig)

    colors = {
        "under_damped": "royalblue",
        "critically_damped": "orangered",
        "over_damped": "forestgreen",
    }
    
    for idx, ti in enumerate(t):
        lines = []
        for label, data in zip(['under_damped', 'critically_damped', 'over_damped'],
                              [u_damped, c_damped, o_damped]):

            c = colors[label]
            l, = ax.plot(t[:idx+1], data[:idx+1], color=c, label=label)
            ax.scatter(ti, data[idx], color=c)
            ax.hlines(0, 0, T, color="black", linestyle="dashed")

            lines.append(l)
        
        ax.legend(handles=lines)
        
        camera.snap()

    anim = camera.animate()
    plt.close()

    gif_path = ROOT / "damped_osc.gif"  
    anim.save(gif_path, writer="pillow", fps=30)
    return Image(url=gif_path)

damped_osc()