I would like to investigate some spring physics. First let’s consider the one dimensional case. The spring force can be modeled as:
\[F = -kx\]where $k$ is the spring constant. Using Newton’s second law:
\[\begin{align*} F &= ma\\ ma &= -kx\\ a &= -\frac{k}{m}x \end{align*}\]If we define $\omega^2 = \frac{k}{m}$, then we have:
\[\begin{align*} \frac{d^2{x}}{dt^2} = -\omega^2x \end{align*}\]which is a second-order differential equation. A solution is:
\[x = A\cos(\omega t+\phi)\]where $A$ and $\phi$ are amplitude and phase, respectively, which are constants that can be determined by initial conditions. The velocity and acceleration can be determined by differentiating the position equation:
\[v = -A\omega\sin(\omega t+\phi)\\ a = -A\omega^2\cos(\omega t + \phi)\]What this looks like:
from pathlib import Path
import os
from IPython.display import HTML, Image
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from celluloid import Camera
from scipy.integrate import odeint
from matplotlib.patches import Circle
ROOT = Path("./assets/img/")
if not os.path.exists(ROOT):
os.makedirs(ROOT)
def to_cartesian(R, theta, phi):
x = R*np.sin(np.deg2rad(theta))*np.cos(np.deg2rad(phi))
y = R*np.sin(np.deg2rad(theta))*np.sin(np.deg2rad(phi))
z = R*np.cos(np.deg2rad(theta))
return x, y, z
def spring1d():
omega = 1 # rad/sec
A = 0.1 # m
T = 3*1/omega*2*np.pi
t = np.linspace(0, T, 100)
x = A*np.cos(omega*t)
fig, (ax_mass, ax_graph) = plt.subplots(1, 2, figsize=(12,5))
ax_graph.set_xlabel("t")
ax_graph.set_ylabel("x")
ax_graph.set_xlim((0, T))
ax_graph.set_ylim((-0.2,0.2))
xmin = -0.2
xmax = 0.2
ymin = -0.1
ymax = 1.0
ax_mass.set_xlim((xmin, xmax))
ax_mass.set_ylim((ymin, ymax))
ax_mass.set_yticks([])
mass_width = 0.08
mass_height = 0.2
wall_x = -0.19
camera = Camera(fig)
for idx, ti in enumerate(t):
ax_mass.hlines(0, xmin, xmax, color="black")
ax_mass.vlines(0, ymin, ymax, color="black", linestyle="dashed")
ax_mass.vlines(wall_x, ymin, ymax, color="black")
_x = x[idx]-mass_width/2.
rect = patches.Rectangle((_x, 0.01), 0.08, 0.2, linewidth=1, edgecolor='black', facecolor='none')
ax_mass.add_patch(rect)
ax_mass.hlines(mass_height/2., wall_x, _x, color="black")
ax_graph.plot(t[:idx+1], x[:idx+1], color="royalblue", label="x")
ax_graph.scatter(ti, x[idx], color="royalblue")
ax_graph.hlines(0, 0, T, color="black", linestyle="dashed")
camera.snap()
anim = camera.animate()
plt.close()
gif_path = ROOT / "spring1d.gif"
anim.save(gif_path, writer="pillow", fps=30)
return Image(url=gif_path)
spring1d()
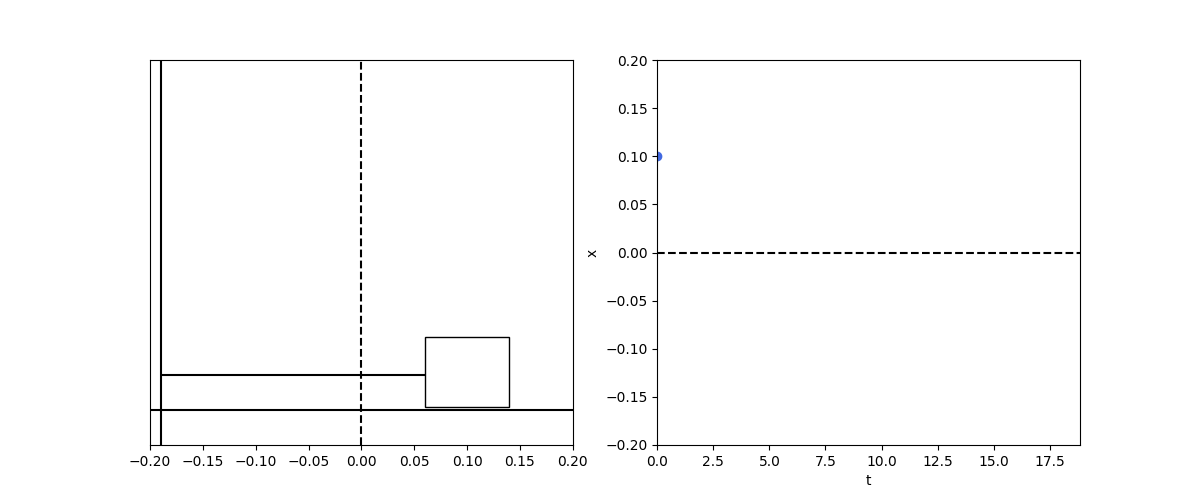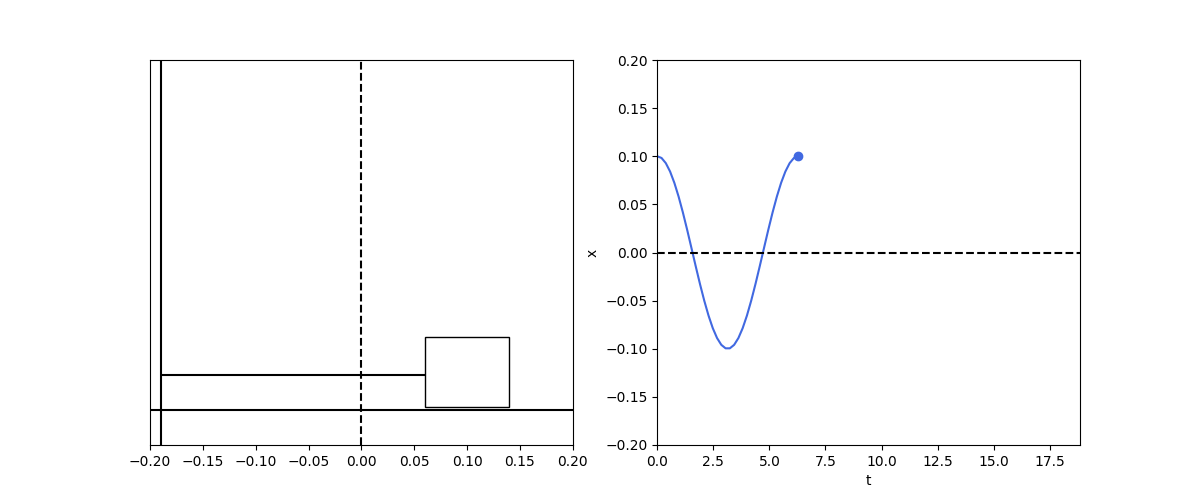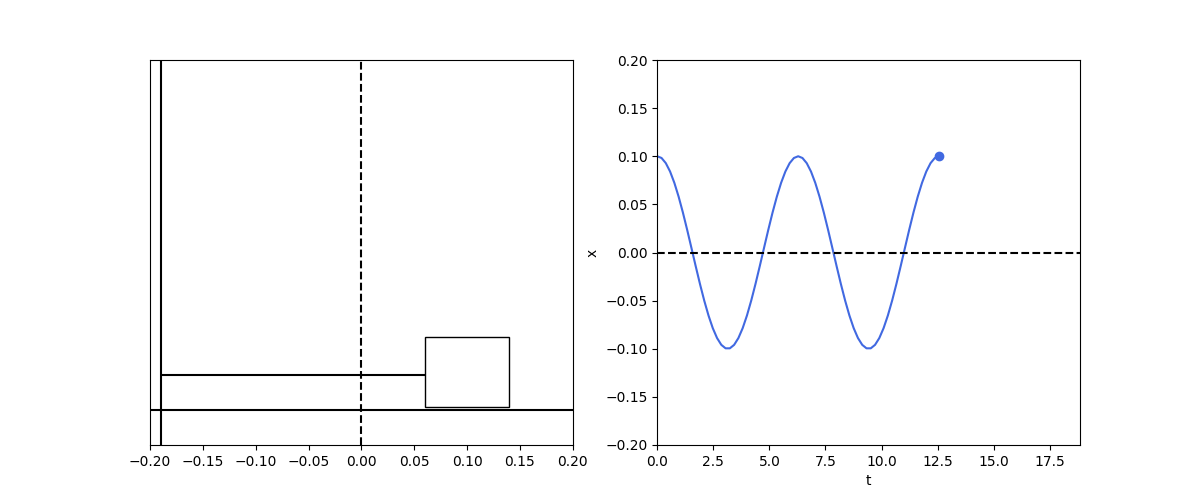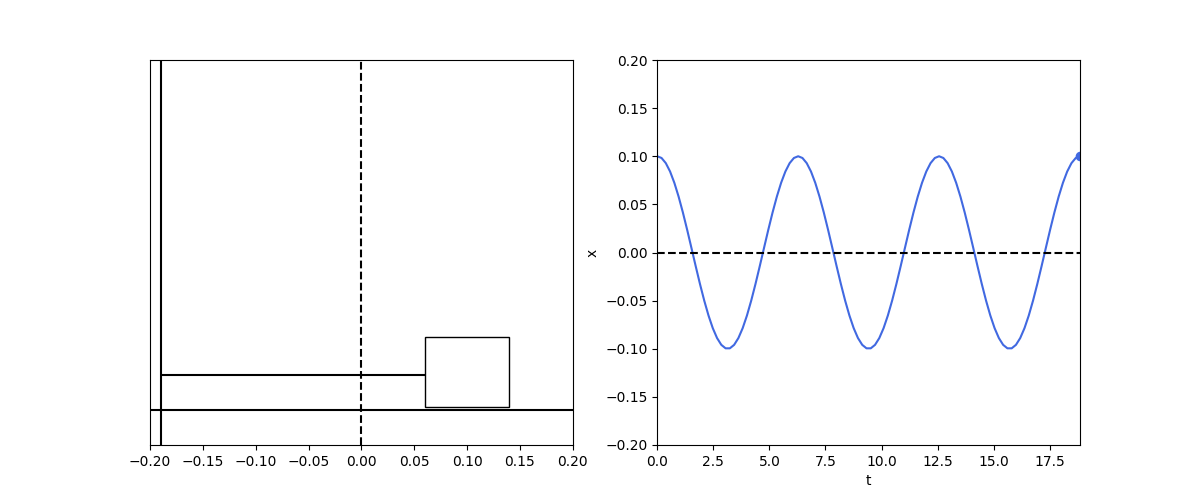
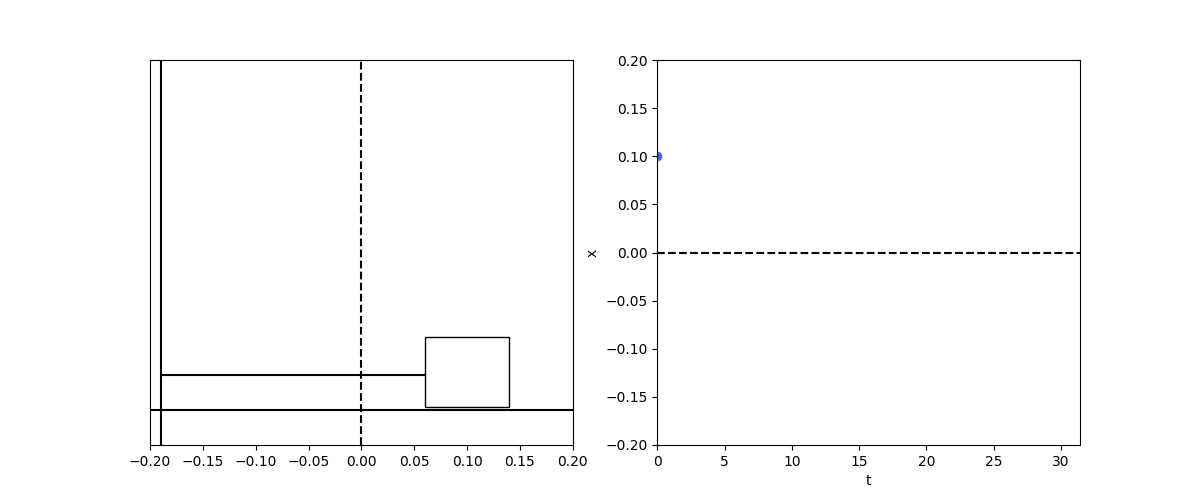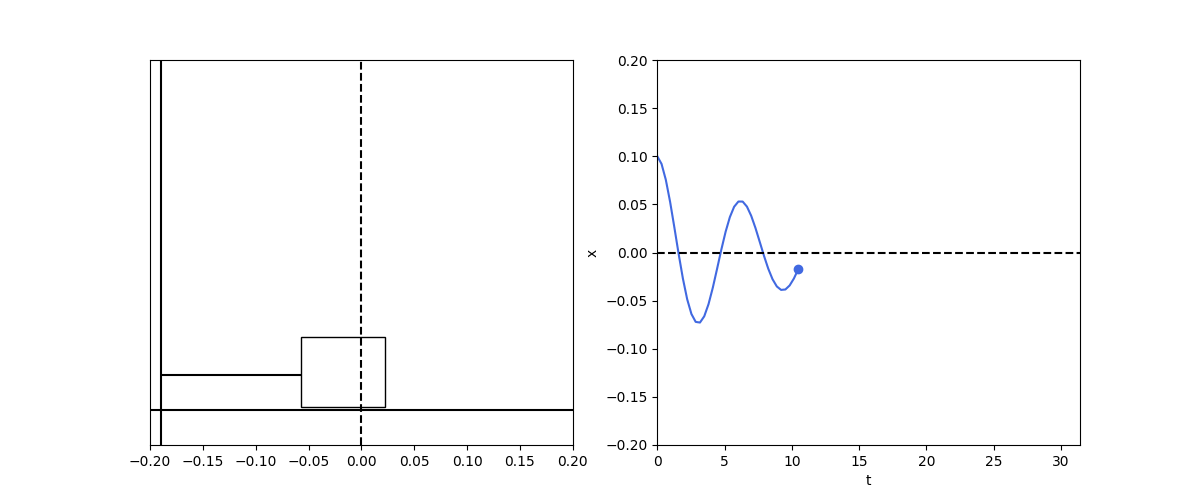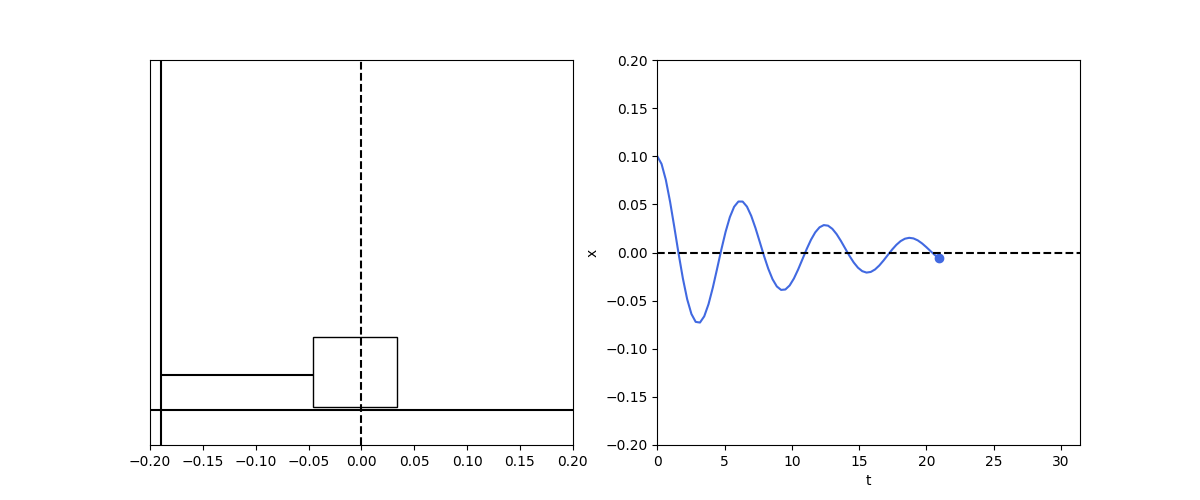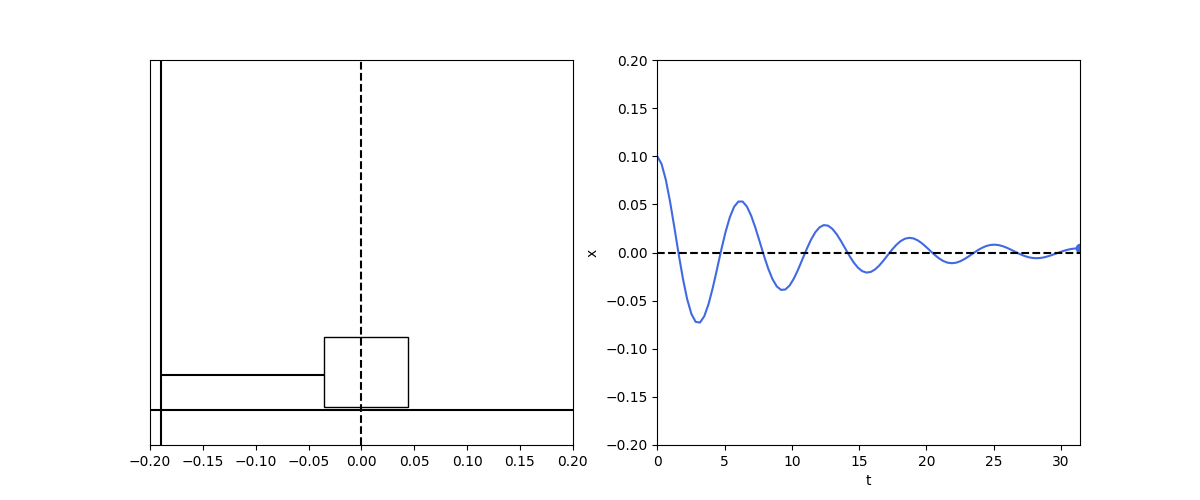
This is the infamous harmonic osillation. As the mass is displaced from the spring equilibrium position, the restoring force increases. This decelerates the mass till it stops completely and reverse direction and starts accelerating in the other direction. As the mass crosses the equilibrium position, a restoring force kicks in in the other direction and so on.
As you may imagine, this will continue for eternity if not disturbed, which is not in agreement with our everyday experience of the physical world. Hence, this is an idealization (at least for the macro phenomenon) that lives only in a platonic realm. In reality, in addition to the restoring force, there are also resitive forces, such as friction, whcih interfere with that happening.
We can add the contribution of resitive force as:
\[F = -kx - b v\]where $b$ is a constant. The resistive force is represented by the second term, which depends on velocity. So, when the object is not moving, it does not experience a resistive force (which is reasonable) and the magnitude of the force will depend on the speed of the object (so higher speed $\rightarrow$ larger resistance).
Same way, using Newton second law to deduce the equation of motion:
\[\frac{d^2x}{dt^2} + \frac{b}{m} \frac{dx}{dt} + \frac{k}{m} x = 0\]When the resistive force is weaker than the restoring force, we get the underdamped oscillator:
\[x(t) = A e^{-\frac{b}{2m} t} \cos(\omega t + \phi)\]def damped_spring1d():
k = 1
m = 1
omega = np.sqrt(k/m) # rad/sec
A = 0.1 # m
b = 0.2
T = 5*1/omega*2*np.pi
t = np.linspace(0, T, 100)
x = A*np.exp(-b/(2*m)*t)*np.cos(omega*t)
fig, (ax_mass, ax_graph) = plt.subplots(1, 2, figsize=(12,5))
ax_graph.set_xlabel("t")
ax_graph.set_ylabel("x")
ax_graph.set_xlim((0, T))
ax_graph.set_ylim((-0.2,0.2))
xmin = -0.2
xmax = 0.2
ymin = -0.1
ymax = 1.0
ax_mass.set_xlim((xmin, xmax))
ax_mass.set_ylim((ymin, ymax))
ax_mass.set_yticks([])
mass_width = 0.08
mass_height = 0.2
wall_x = -0.19
camera = Camera(fig)
for idx, ti in enumerate(t):
ax_mass.hlines(0, xmin, xmax, color="black")
ax_mass.vlines(0, ymin, ymax, color="black", linestyle="dashed")
ax_mass.vlines(wall_x, ymin, ymax, color="black")
_x = x[idx]-mass_width/2.
rect = patches.Rectangle((_x, 0.01), 0.08, 0.2, linewidth=1, edgecolor='black', facecolor='none')
ax_mass.add_patch(rect)
ax_mass.hlines(mass_height/2., wall_x, _x, color="black")
ax_graph.plot(t[:idx+1], x[:idx+1], color="royalblue", label="x")
ax_graph.scatter(ti, x[idx], color="royalblue")
ax_graph.hlines(0, 0, T, color="black", linestyle="dashed")
camera.snap()
anim = camera.animate()
plt.close()
gif_path = ROOT / "damped_spring1d.gif"
anim.save(gif_path, writer="pillow", fps=30)
return Image(url=gif_path)
damped_spring1d()
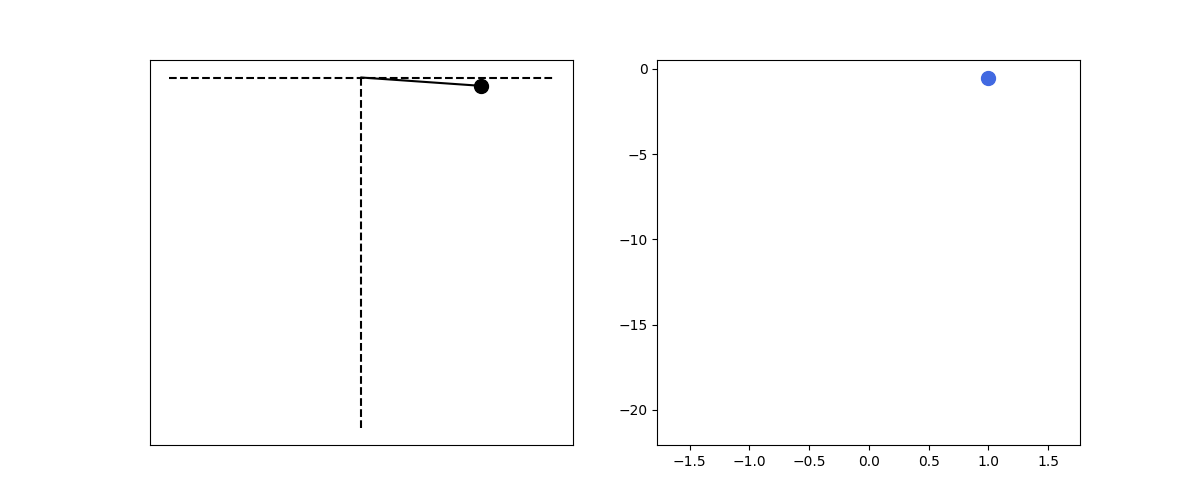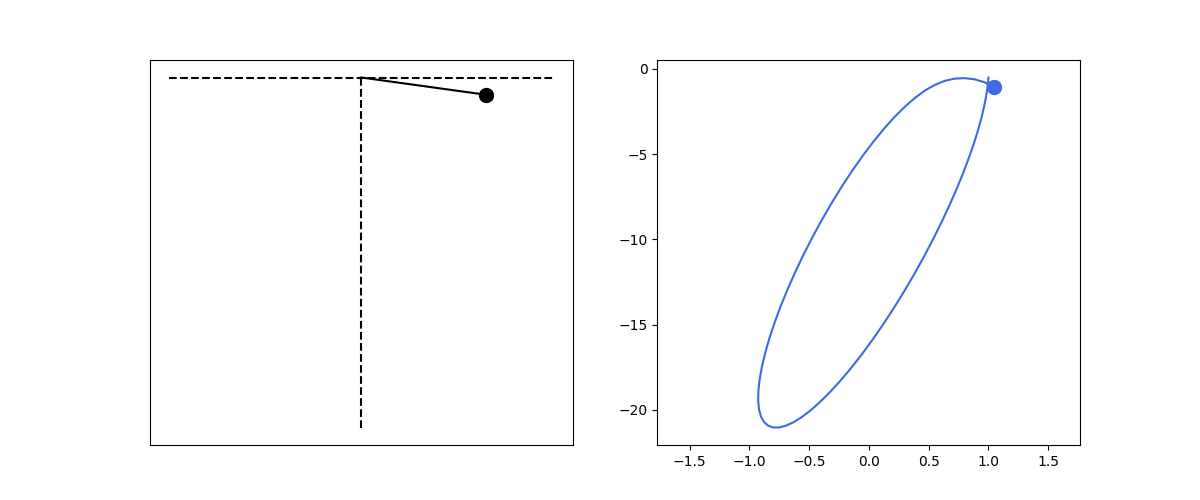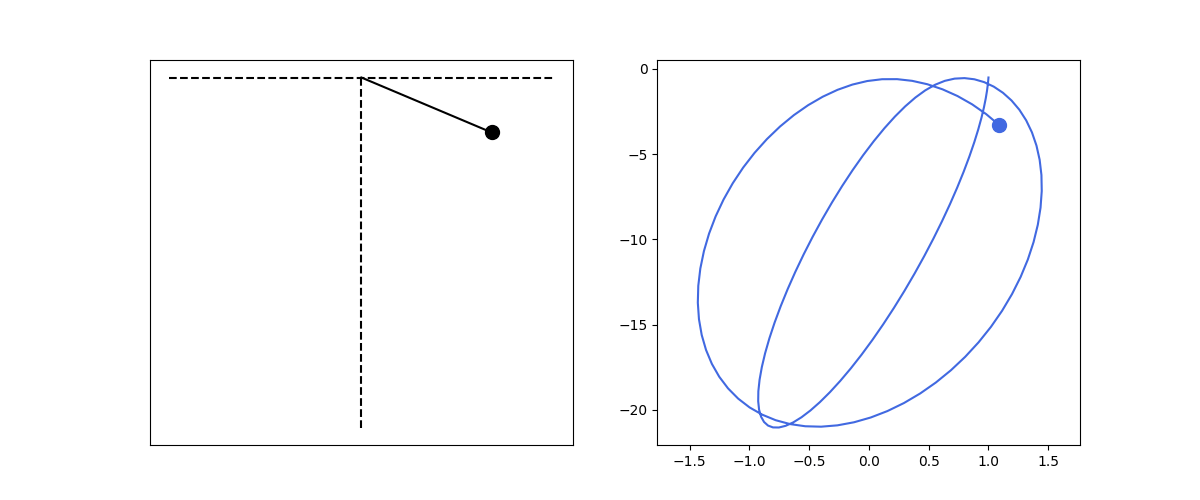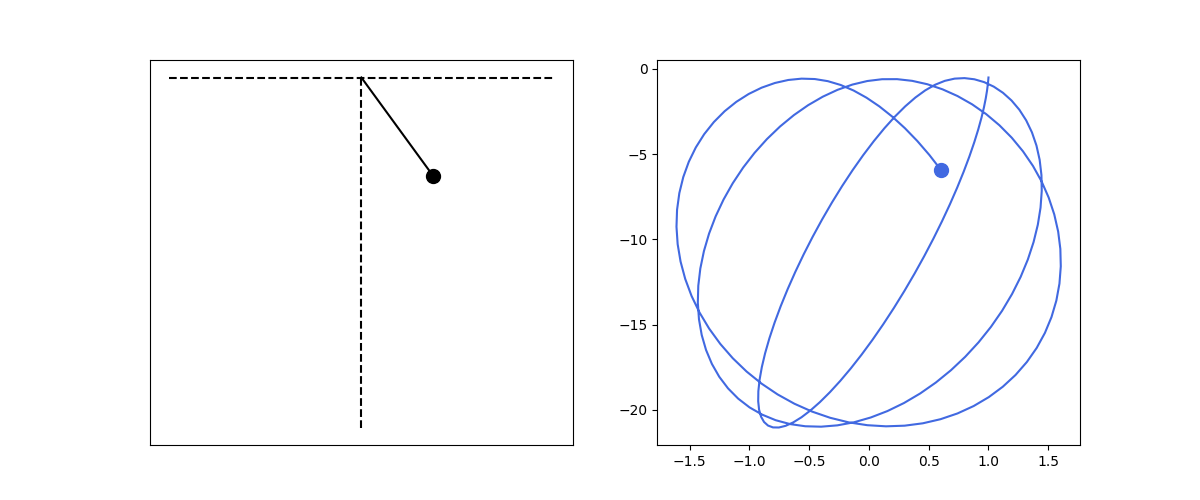
Let’s consider simulations in 2D. First, let’s assume a mass fixed to ceiling by a spring and free to move in two dimensions under the influence of the spring force and gravity. Let the mass poition be represented by the vector $\textbf{r}$, the fixation point is the origin, gravity acceleration is $\textbf{g} = -g \hat{\textbf{j}}$, where $g = 9.8$, the unstretched spring length is $l$ and $\hat{\textbf{r}}$ is the unit vector in the direction along the spring. Then:
\[\frac{d^2\textbf{r}}{dt^2} = -\frac{k}{m}(|\textbf{r}| - l) \hat{\textbf{r}} + \frac{1}{m} \textbf{g}\]To solve numerically, we may represent the previous motion equation as:
\[\begin{align*} |\textbf{r}| &= \sqrt{x^2 + y^2}\\\\ \frac{d\textbf{v}}{dt} &= -\frac{k}{m}(|\textbf{r}| - l) \hat{\textbf{r}} + \frac{1}{m} \textbf{g} \\\\ \frac{d\textbf{r}}{dt} &= \textbf{v} \end{align*}\]def hanged_spring2d():
k = 1
m = 1
g = np.array([0, -9.8])
l = 1
r0 = np.array([1, -.5])
v0 = np.array([0, 0.])
s0 = np.concat((r0, v0))
def motion_fn(s, t):
r0, v0 = s[:2], s[2:]
r_abs = np.linalg.norm(r0)
dv = -k/m*(r_abs - l)*r0/r_abs + 1/m*g
dr = v0
return np.concat([dr, dv])
t = np.linspace(0, 20, 200)
sol = odeint(motion_fn, s0, t)
fig, (ax_mass, ax_graph) = plt.subplots(1, 2, figsize=(12,5))
ax_mass.set_xticks([])
ax_mass.set_yticks([])
xmax = np.abs(sol[:,0]).max()
ymax = np.abs(sol[:,1]).max()
camera = Camera(fig)
for t_idx in range(len(sol)):
x, y = sol[t_idx, :2]
ax_mass.scatter(x, y, color="black", s=100)
ax_mass.plot(np.array([0, x]), np.array([0, y]), color="black")
ax_mass.hlines(0, -xmax, xmax, color="black", linestyle="dashed")
ax_mass.vlines(0, -ymax, 0, color="black", linestyle="dashed")
ax_graph.scatter(x, y, color="royalblue", s=100)
ax_graph.plot(sol[:t_idx+1, 0], sol[:t_idx+1, 1], color="royalblue")
camera.snap()
anim = camera.animate()
plt.close()
gif_path = ROOT / "hanged_spring2d.gif"
anim.save(gif_path, writer="pillow", fps=30)
return Image(url=gif_path)
hanged_spring2d()
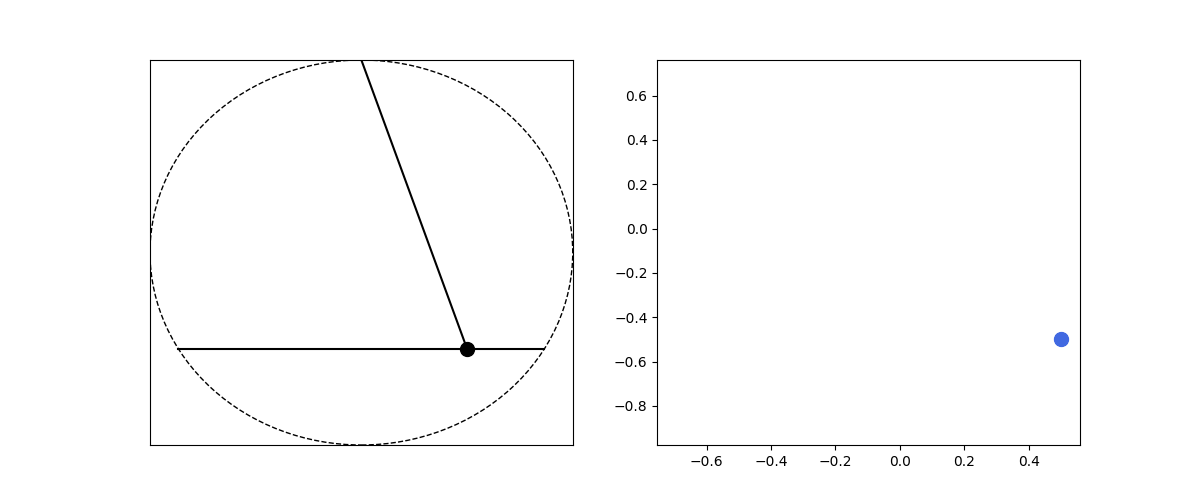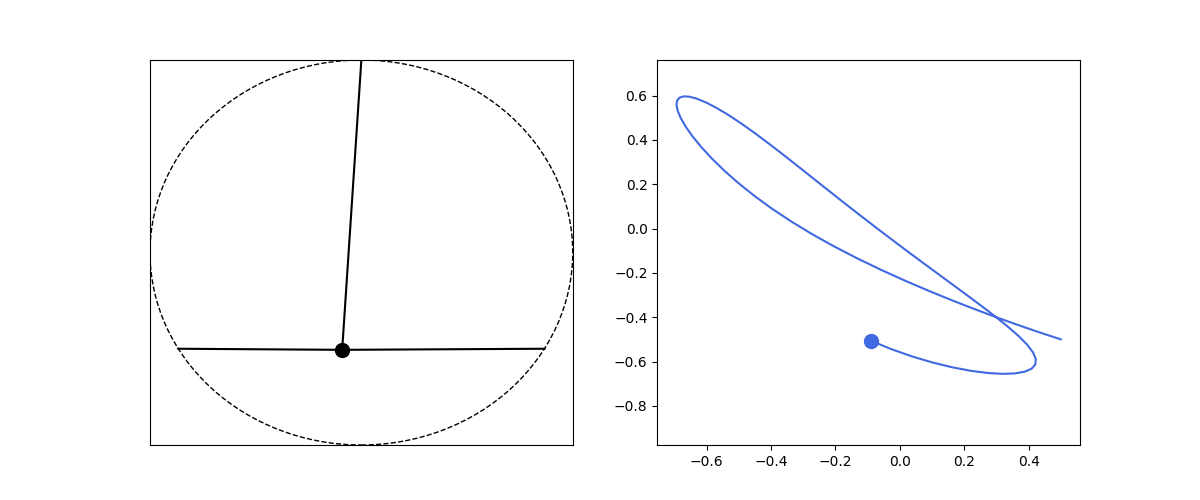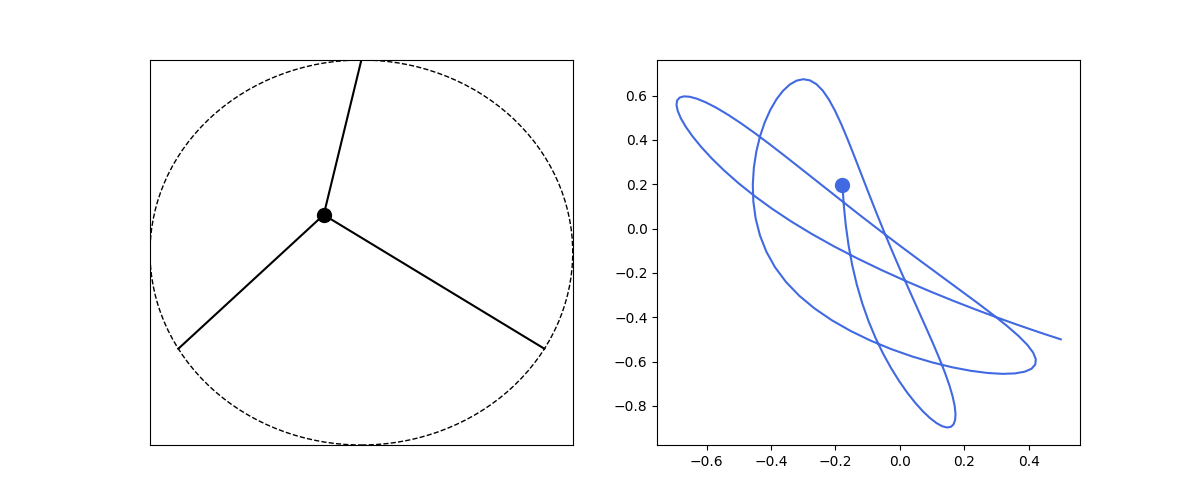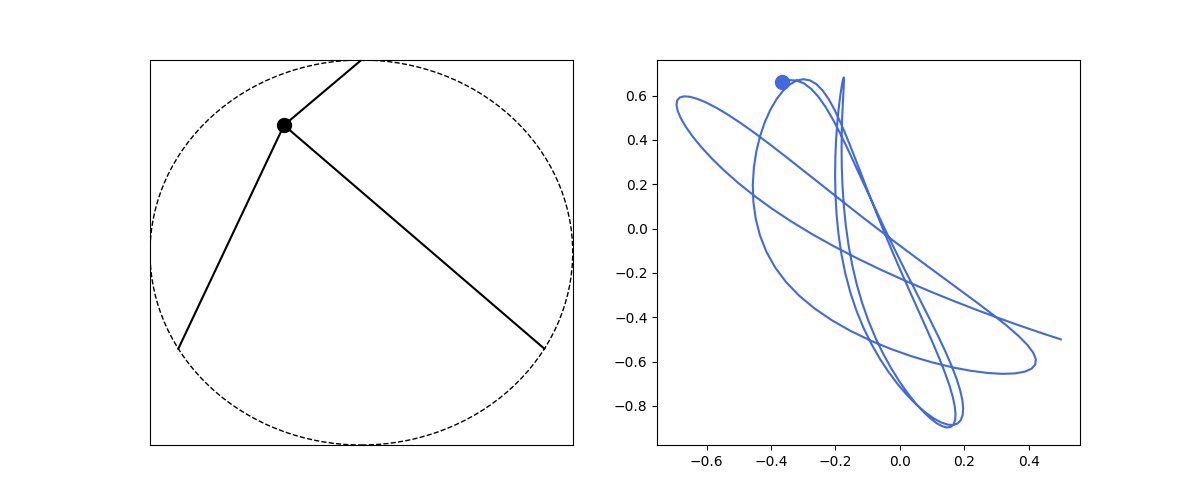
Let’s make this more interesting by including multiple springs. To simplify, let’s ignore gravity influence. Let’s consider the following arrangment. Mass is at the center of a circle with radius $R$, multiple springs are attached to the mass at one end and to a point on the circle circumference on the other end. Let the spring attach points be $\textbf{r}_i$, the mass position to be $r$ and the unstretched length of any spring to be $R$. Then our equation of motion is:
\[\frac{d^2\textbf{r}}{dt^2} = \frac{k}{m} \sum_i (R-|\textbf{r} - \textbf{r}_i|)\frac{\textbf{r} - \textbf{r}_i}{|\textbf{r} - \textbf{r}_i|}\]and we rewrite for numerical simulation:
\[\begin{align*} \frac{d\textbf{v}}{dt} &= \frac{k}{m} \sum_i (R-|\textbf{r} - \textbf{r}_i|)\frac{\textbf{r} - \textbf{r}_i}{|\textbf{r} - \textbf{r}_i|}\\\\ \frac{d\textbf{r}}{dt} &= \textbf{v} \end{align*}\]def circle_spring2d():
k = 1
m = 1
R = 1
r0 = np.array([.5, -.5])
v0 = np.array([0, 0.])
s0 = np.concat((r0, v0))
fix_points = np.array([[R*np.sin(np.deg2rad(theta)), R*np.cos(np.deg2rad(theta))] for theta in [0, 120, 240]])
def motion_fn(s, t):
r0, v0 = s[:2], s[2:]
dv = 0.
for ri in fix_points:
norm = np.linalg.norm(r0 - ri)
dv += (R - norm)*(r0-ri)/norm
dv *= k/m
dr = v0
return np.concat([dr, dv])
t = np.linspace(0, 20, 200)
sol = odeint(motion_fn, s0, t)
fig, (ax_mass, ax_graph) = plt.subplots(1, 2, figsize=(12,5))
ax_mass.set_xticks([])
ax_mass.set_yticks([])
ax_mass.set_xlim((-1, 1))
ax_mass.set_ylim((-1, 1))
camera = Camera(fig)
for t_idx in range(len(sol)):
x, y = sol[t_idx, :2]
ax_mass.scatter(x, y, color="black", s=100)
circle = patches.Circle(xy=(0, 0), radius=R, linestyle="dashed", fill=False)
ax_mass.add_patch(circle)
for ri in fix_points:
ax_mass.plot([x, ri[0]], [y, ri[1]], color="black")
ax_graph.scatter(x, y, color="royalblue", s=100)
ax_graph.plot(sol[:t_idx+1, 0], sol[:t_idx+1, 1], color="royalblue")
camera.snap()
anim = camera.animate()
plt.close()
gif_path = ROOT / "circle_spring2d.gif"
anim.save(gif_path, writer="pillow", fps=30)
return Image(url=gif_path)
circle_spring2d()
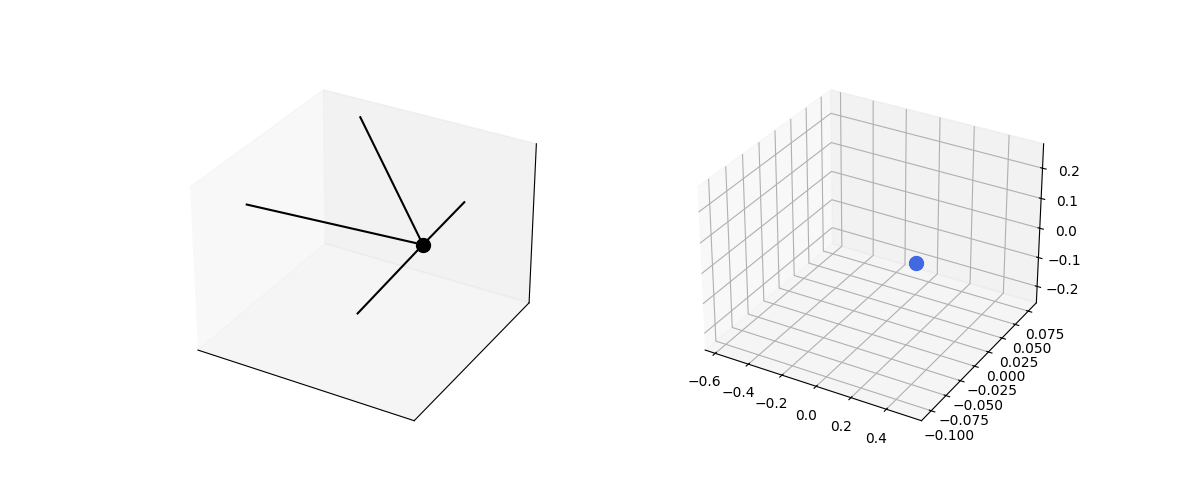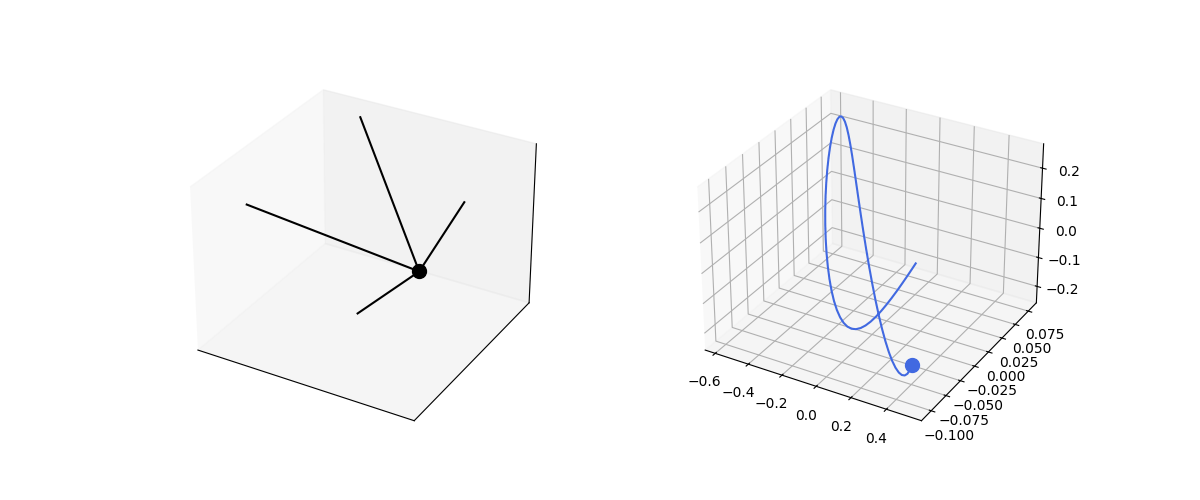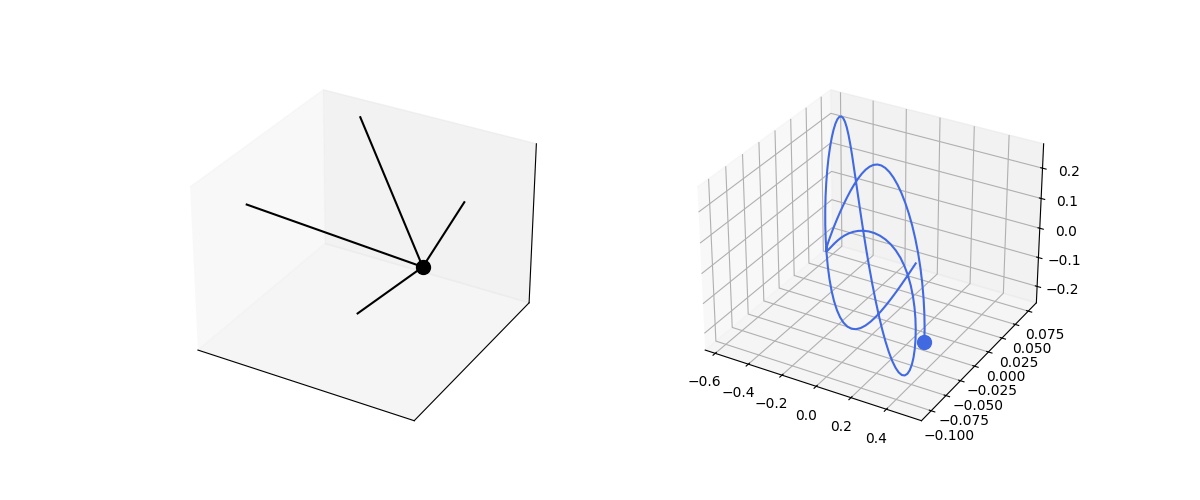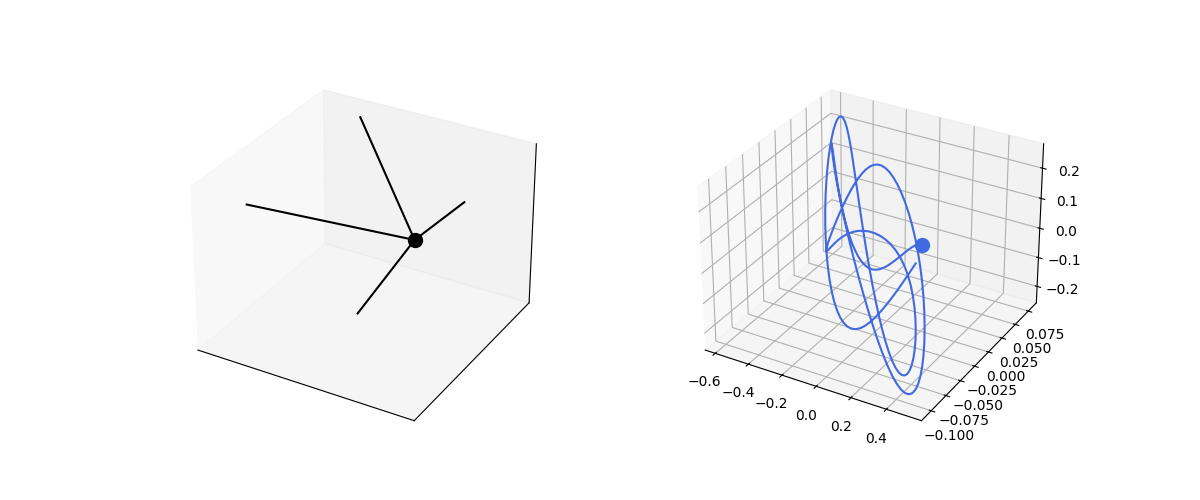
This can be extended trivially to 3D. The same set of equations apply, just now the vectors are 3D.
def sphere_spring3d():
k = 1
m = 1
R = 1
r0 = np.array([.5, -.1, 0.2])
v0 = np.array([0, 0., 0.])
s0 = np.concat((r0, v0))
# inclination, azimuth
fix_points_polar_coords = np.array([[45., 0.], [45., 120.], [45, 240.], [180., 0.]])
fix_points = []
for theta, phi in fix_points_polar_coords:
x = R*np.sin(np.deg2rad(theta))*np.cos(np.deg2rad(phi))
y = R*np.sin(np.deg2rad(theta))*np.sin(np.deg2rad(phi))
z = R*np.cos(np.deg2rad(theta))
fix_points.append([x, y, z])
fix_points = np.array(fix_points)
def motion_fn(s, t):
r0, v0 = s[:3], s[3:]
dv = 0.
for ri in fix_points:
norm = np.linalg.norm(r0 - ri)
dv += (R - norm)*(r0-ri)/norm
dv *= k/m
dr = v0
return np.concat([dr, dv])
t = np.linspace(0, 20, 200)
sol = odeint(motion_fn, s0, t)
fig = plt.figure(figsize=(12, 5))
ax_mass = fig.add_subplot(1, 2, 1, projection='3d')
ax_mass.set_xticks([])
ax_mass.set_yticks([])
ax_mass.set_zticks([])
ax_graph = fig.add_subplot(1, 2, 2, projection='3d')
camera = Camera(fig)
for t_idx in range(len(sol)):
x, y, z = sol[t_idx, :3]
ax_mass.scatter(x, y, z, color="black", s=100)
for ri in fix_points:
ax_mass.plot([x, ri[0]], [y, ri[1]], [z, ri[2]], color="black")
ax_graph.scatter(x, y, z, color="royalblue", s=100)
ax_graph.plot(sol[:t_idx+1, 0], sol[:t_idx+1, 1], sol[:t_idx+1, 2], color="royalblue")
camera.snap()
anim = camera.animate()
plt.close()
gif_path = ROOT / "sphere_spring3d.gif"
anim.save(gif_path, writer="pillow", fps=30)
return Image(url=gif_path)
sphere_spring3d()
So far the system dynamics evolution was due to the spring forces and (optionally) gravity. However, we can model any other external forces acting on the system:
\[\frac{d^2\textbf{r}}{dt^2} = \frac{k}{m} \sum_i (R-|\textbf{r} - \textbf{r}_i|)\frac{\textbf{r} - \textbf{r}_i}{|\textbf{r} - \textbf{r}_i|} + \frac{1}{m}\sum_j\textbf{F}_j\]A special case to that would be central forces:
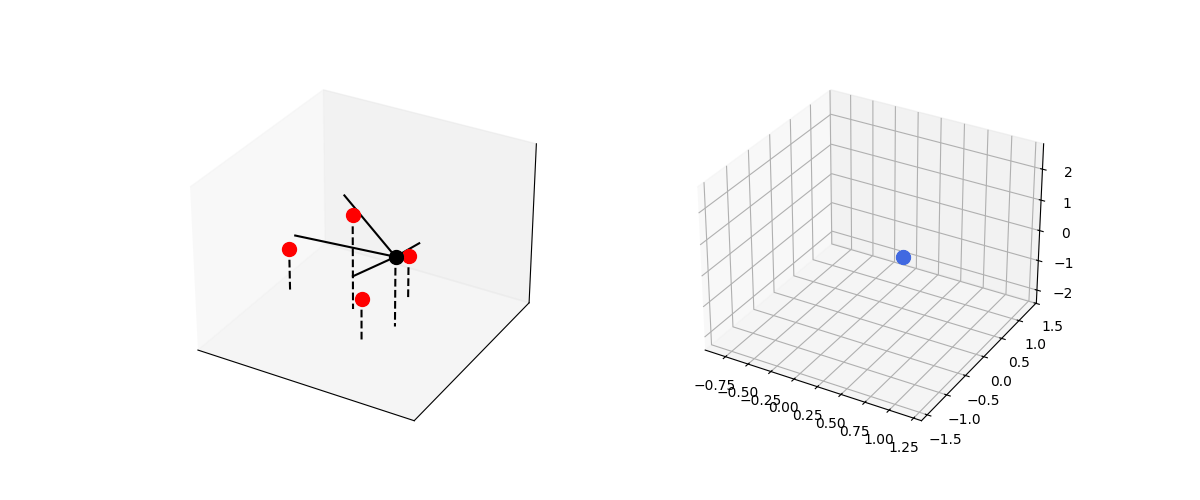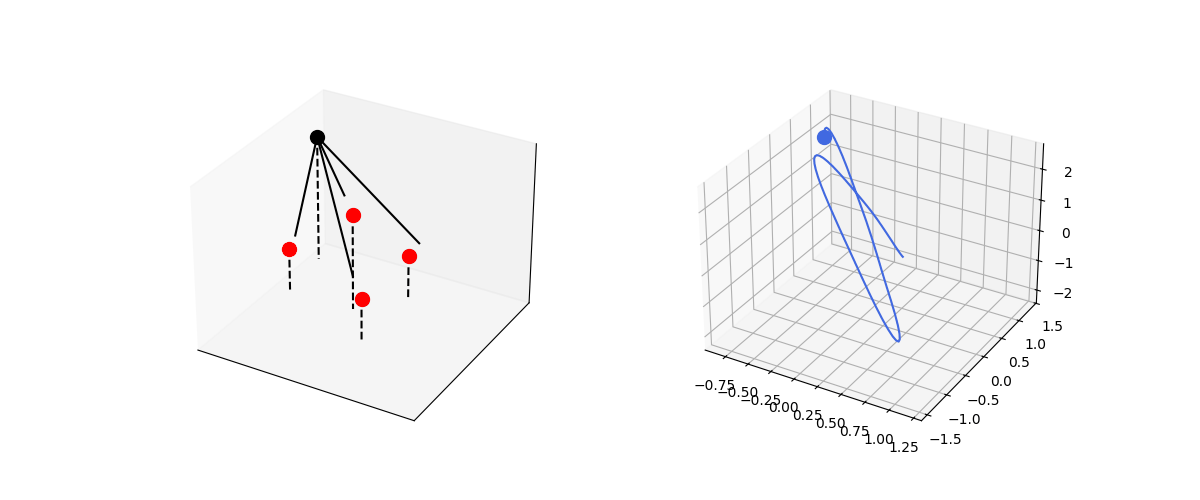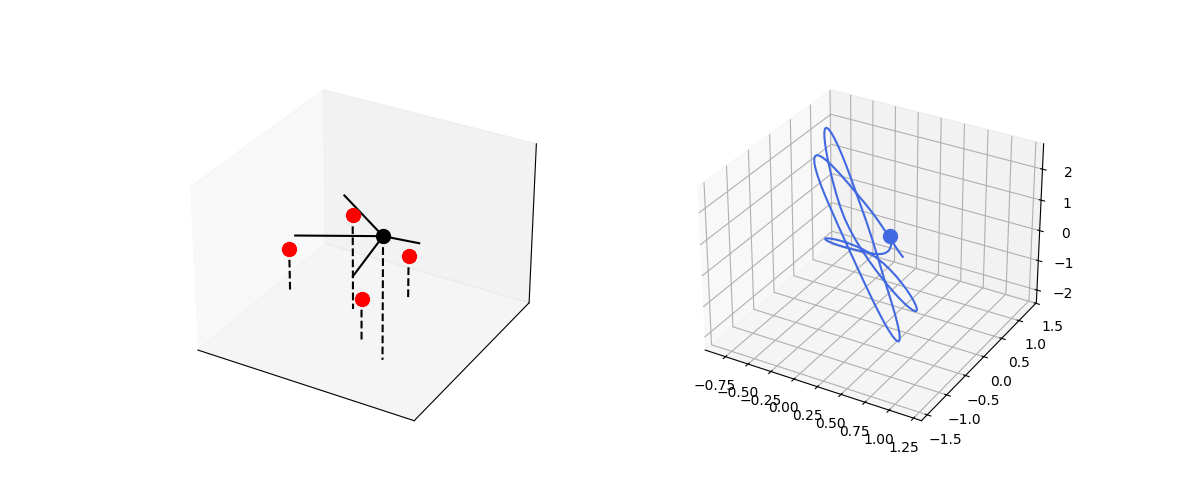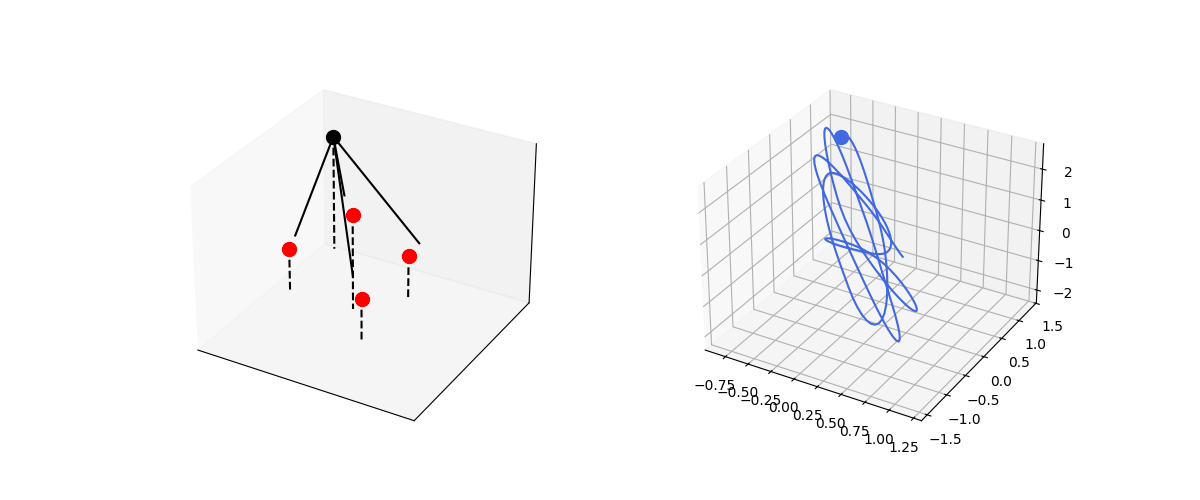
\[\frac{d^2\textbf{r}}{dt^2} = \frac{k}{m} \sum_i (R-|\textbf{r} - \textbf{r}_i|)\frac{\textbf{r} - \textbf{r}_i}{|\textbf{r} - \textbf{r}_i|} + \frac{1}{m}\sum_j F_j \frac{\textbf{r} - \textbf{r}_j}{|\textbf{r} - \textbf{r}_j|}\]To make the dynamics more interesting, let’s model a varying force:
\[F = A \sin(\omega t + \phi)\]Let’s realize this by a set of objects that exert central force on the spring-mass system.
def central_spring3d():
k = 1
m = 1
R = 1
r0 = np.array([.5, -.1, 0.2])
v0 = np.array([0, 0., 0.])
s0 = np.concat((r0, v0))
# inclination, azimuth
fix_points_polar_coords = np.array([[45., 0.], [45., 120.], [45, 240.], [180., 0.]])
fix_points = []
for theta, phi in fix_points_polar_coords:
fix_points.append(to_cartesian(R, theta, phi))
fix_points = np.array(fix_points)
objects_polar_coords = np.array([[135., 60.], [135, 180.], [135, 300.], [0., 0.]])
objects = []
for theta, phi in objects_polar_coords:
objects.append(to_cartesian(R, theta, phi))
A = 1.
omega = 1.
object_phases = np.array([0., 25, 45, 60.])
def motion_fn(s, t):
r0, v0 = s[:3], s[3:]
dv = 0.
for ri in fix_points:
norm = np.linalg.norm(r0 - ri)
dv += (R - norm)*(r0-ri)/norm
dv *= k/m
for idx, ri in enumerate(objects):
norm = np.linalg.norm(r0 - ri)
dv += A*np.sin(omega*t+object_phases[idx])*(r0-ri)/norm
dv *= 1/m
dr = v0
return np.concat([dr, dv])
t = np.linspace(0, 20, 200)
sol = odeint(motion_fn, s0, t)
zmin = sol[:,2].min()
fig = plt.figure(figsize=(12, 5))
ax_mass = fig.add_subplot(1, 2, 1, projection='3d')
ax_mass.set_xticks([])
ax_mass.set_yticks([])
ax_mass.set_zticks([])
ax_graph = fig.add_subplot(1, 2, 2, projection='3d')
camera = Camera(fig)
for t_idx in range(len(sol)):
x, y, z = sol[t_idx, :3]
ax_mass.scatter(x, y, z, color="black", s=100)
ax_mass.plot([x,x], [y,y], [z,zmin], linestyle="dashed", color="black")
for ri in fix_points:
ax_mass.plot([x, ri[0]], [y, ri[1]], [z, ri[2]], color="black")
for ri in objects:
ax_mass.scatter(ri[0], ri[1], ri[2], color="red", s=100)
ax_mass.plot([ri[0], ri[0]],[ri[1],ri[1]], [ri[2],zmin],
linestyle="dashed", color="black")
ax_graph.scatter(x, y, z, color="royalblue", s=100)
ax_graph.plot(sol[:t_idx+1, 0], sol[:t_idx+1, 1], sol[:t_idx+1, 2], color="royalblue")
camera.snap()
anim = camera.animate()
plt.close()
gif_path = ROOT / "central_spring3d.gif"
anim.save(gif_path, writer="pillow", fps=30)
return Image(url=gif_path)
central_spring3d()
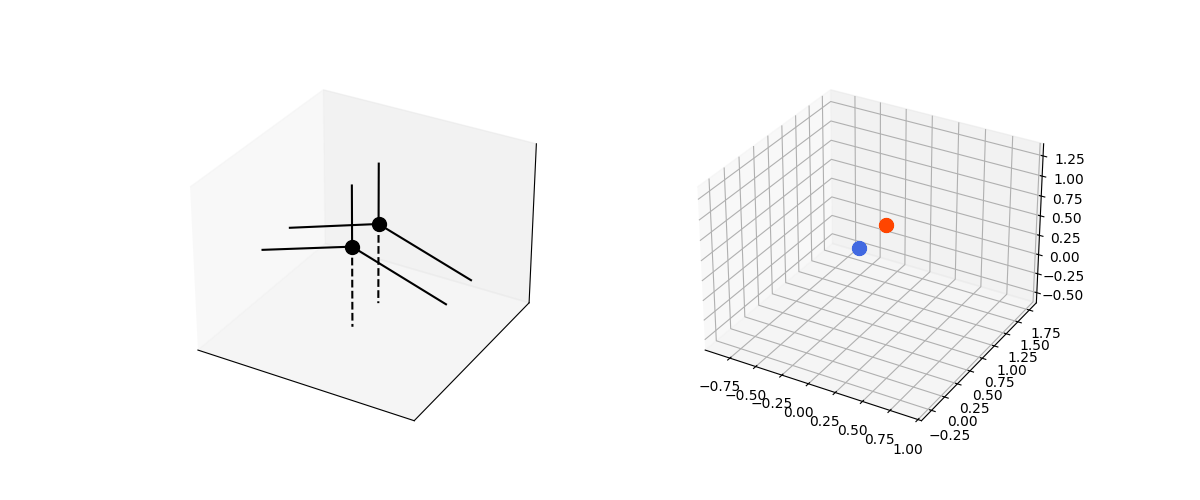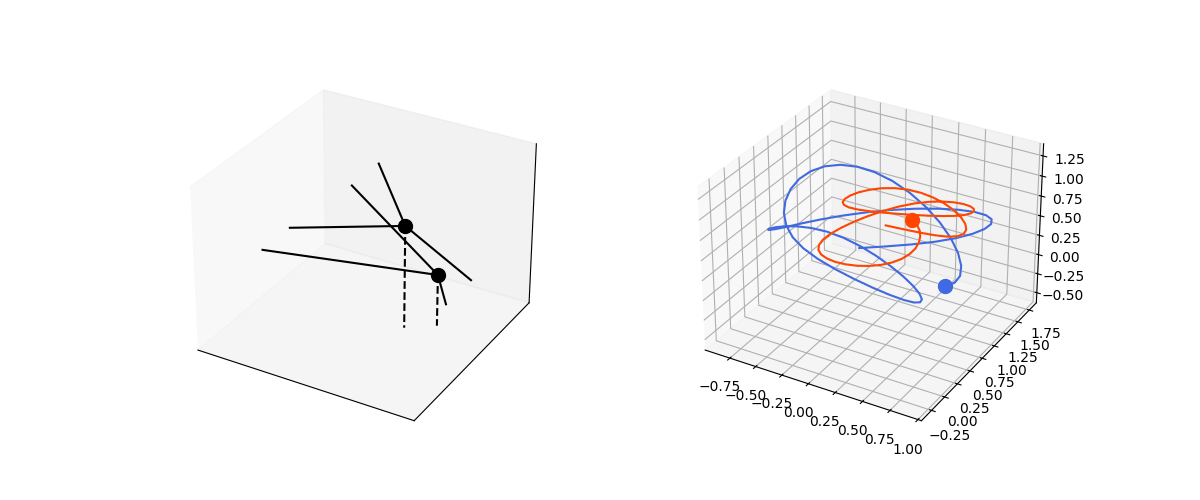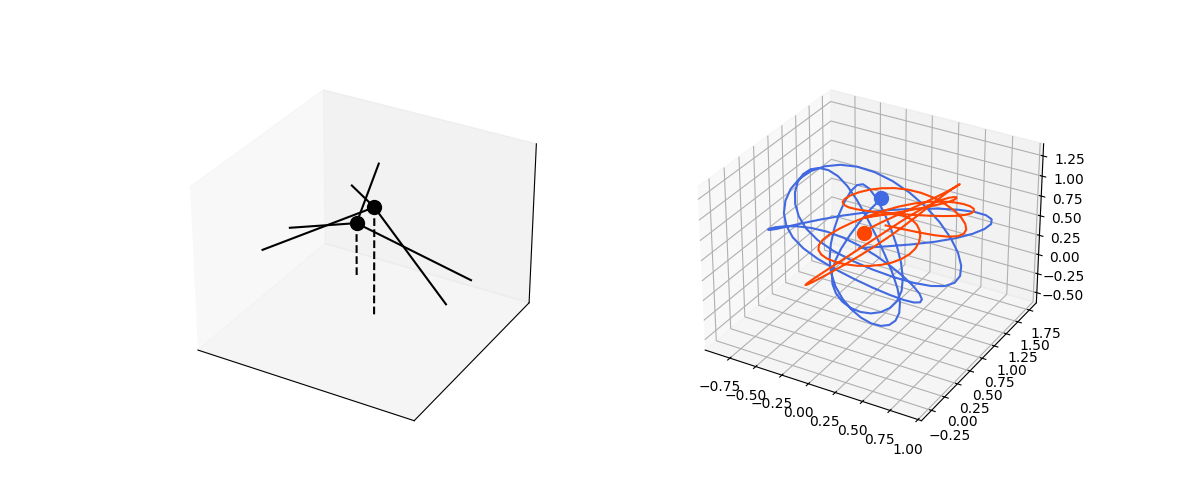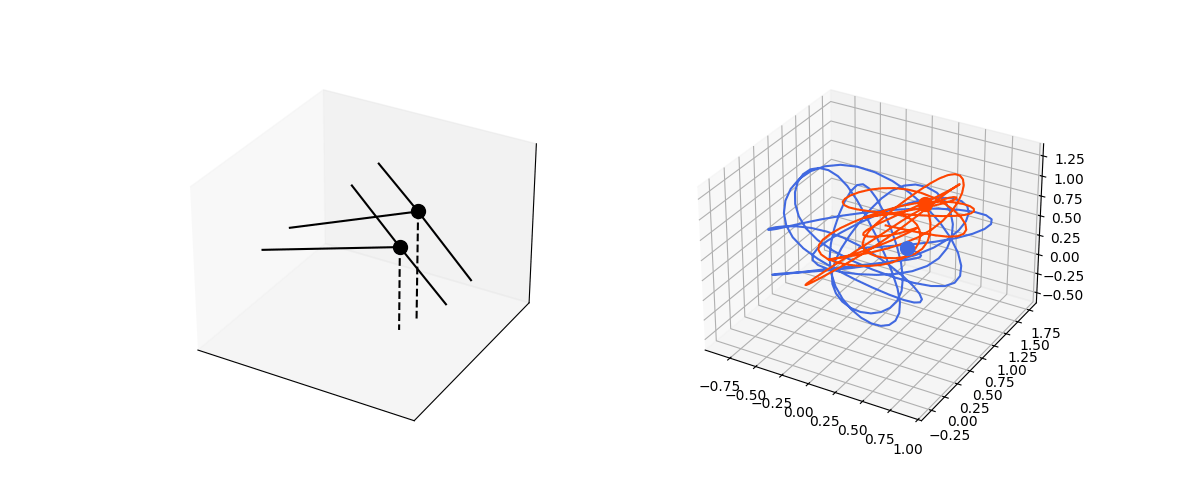
We can extend this to multiple string systems interacting with each others. For example, two spring systems with attractive forces between the masses.
class SpringSystem:
def __init__(self, fix_points: np.ndarray, R, k, m):
self.fix_points = fix_points
self.R = R
self.k = k
self.m = m
def __call__(self, r, v, t, f):
dv = 0.
for ri in self.fix_points:
norm = np.linalg.norm(r - ri)
dv += (self.R - norm)*(r-ri)/norm
dv *= self.k/self.m
dv += 1/self.m*f
dr = v
return dr, dv
def multiple_spring3d():
k = 1
m = 1
R = 1
F = 0.01
r0 = np.array([[.0, .5, 0.5], [0., 1., .5]])
v0 = np.array([[1., 0.5, .2], [0.8, 0.1, 0.]])
# azimuth, inclination
fix_points_inclination = np.array([[0., 0.],[0., 120.], [0., -120.]])
fix_points_to_origin = []
for az, inc in fix_points_inclination:
x, y, z = to_cartesian(R=R, theta=inc, phi=az)
fix_points_to_origin.append([x,y,z])
fix_points_to_origin = np.array(fix_points_to_origin)
fix_points = []
for _r in r0:
spring_fix_points = []
for point in fix_points_to_origin:
spring_fix_points.append(_r + point)
fix_points.append(spring_fix_points)
fix_points = np.array(fix_points)
s0 = np.concat((r0, v0)).flatten()
spring1 = SpringSystem(fix_points=fix_points[0], R=R, k=k, m=m)
spring2 = SpringSystem(fix_points=fix_points[1], R=R, k=k, m=m)
def motion_fn(s, t):
r1, r2, v1, v2 = s[:3], s[3:6], s[6:9], s[9:]
f12 = (r2-r1)*F
dr1, dv1 = spring1(r1, v1, t, f12)
dr2, dv2 = spring2(r2, v2, t, -f12)
return np.concat([dr1, dr2, dv1, dv2]).flatten()
T = 40
t = np.linspace(0, T, 200)
sol = odeint(motion_fn, s0, t)
zmin = sol[:,:6].min()
fig = plt.figure(figsize=(12, 5))
ax_mass = fig.add_subplot(1, 2, 1, projection='3d')
ax_mass.set_xticks([])
ax_mass.set_yticks([])
ax_mass.set_zticks([])
ax_graph = fig.add_subplot(1, 2, 2, projection='3d')
camera = Camera(fig)
for t_idx in range(len(sol)):
solt = sol[t_idx]
r1, r2 = solt[:3], solt[3:6]
ax_mass.scatter(*r1, color="black", s=100)
ax_mass.scatter(*r2, color="black", s=100)
ax_mass.plot(*zip(r1, [r1[0], r1[1], zmin]), color="black", linestyle="dashed")
ax_mass.plot(*zip(r2, [r2[0], r2[1], zmin]), color="black", linestyle="dashed")
for r, points in zip([r1, r2], [spring1.fix_points, spring2.fix_points]):
for p in points:
ax_mass.plot(*zip(r, p), color="black")
ax_graph.scatter(solt[0], solt[1], solt[2], color="royalblue", s=100)
ax_graph.plot(sol[:t_idx+1, 0], sol[:t_idx+1, 1], sol[:t_idx+1, 2], color="royalblue")
ax_graph.scatter(solt[3], solt[4], solt[5], color="orangered", s=100)
ax_graph.plot(sol[:t_idx+1, 3], sol[:t_idx+1, 4], sol[:t_idx+1, 5], color="orangered")
camera.snap()
anim = camera.animate()
plt.close()
gif_path = ROOT / "multiple_spring3d.gif"
anim.save(gif_path, writer="pillow", fps=30)
return Image(url=gif_path)
multiple_spring3d()